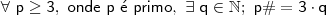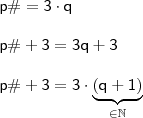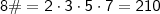por iuggui » Ter Mai 29, 2018 20:42
por iuggui » Ter Mai 29, 2018 20:42
Número primo
[...]
Para todo primo p seja p# o produto de todos os números
primos q inferiores ou iguais a p. De acordo com a terminologia
empregada por Dubner (1987), p# é chamado o primorial de p.[...]
Dadas as afirmativas sobre primoriais de números primos,
considerando estritamente a definição e a simbologia
estabelecidas no texto,
I. O primorial de um número primo é um número primo.
II. Se p é um número primo maior que 2, a soma dos algarismos
do número p# + 3 é um número múltiplo de 3.
III. 8# = 2x3x5x7 = 210.
verifica-se que está(ão) correta(s)
A) I, II e III.
B) I e III, apenas.
C) I e II, apenas.
D) III, apenas.
E) II, apenas.
-
iuggui
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 29, 2018 20:39
- Formação Escolar: PÓS-GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Qui Mai 31, 2018 11:46
por DanielFerreira » Qui Mai 31, 2018 11:46
Olá
Iuggui, seja bem-vindo(a)!
Na
afirmativa I, entendo que seja FALSA, pois de acordo com o texto,
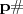
(primordial) é o produto dos números primos menores ou iguais a

. Assim, como exemplo, podemos tomar qualquer primo. Seja
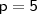
, daí,

Como pode notar, 30 não é primo!
Quanto à
afirmativa II, VERDADEIRA. Veja:
Se

é um primo maior que 3, então o primordial
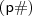
será um múltiplo de 3, com efeito,
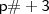
também será múltiplo de 3.
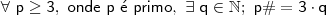
Portanto,
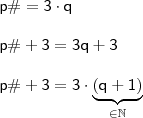
Isto é,
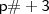
, de fato, é um múltiplo de 3. Logo, temos que a soma de seus algarismos é múltiplo de 3 (regra de divisibilidade por 3).
Por fim, a
afirmativa III:
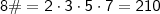
Ou seja, VERDADEIRA!
Não tenho dúvidas que as afirmativas II e III sejam verdadeiras, no entanto, não há essa opção! Com isso, considero a alternativa A)...
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstração (número primo)
por Shetach Hefker » Qui Jan 10, 2013 19:01
- 4 Respostas
- 6521 Exibições
- Última mensagem por Shetach Hefker

Qui Jan 10, 2013 22:48
Aritmética
-
- Como reconhecer se um número é primo?
por Kelvin Brayan » Dom Abr 24, 2011 15:16
- 2 Respostas
- 3547 Exibições
- Última mensagem por Kelvin Brayan

Dom Abr 24, 2011 16:28
Álgebra Elementar
-
- Subgrupo normal e numero primo
por EANDRIOLI » Qua Ago 06, 2014 23:47
- 1 Respostas
- 1890 Exibições
- Última mensagem por adauto martins

Qui Nov 27, 2014 12:13
Álgebra Elementar
-
- Questão, número irracional.
por LuizCarlos » Sex Mar 16, 2012 18:49
- 1 Respostas
- 4055 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 22:27
Álgebra Elementar
-
- Questão de Concurso-Número Complexos
por Pri Ferreira » Qua Mar 21, 2012 13:44
- 1 Respostas
- 1580 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 15:31
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


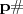 (primordial) é o produto dos números primos menores ou iguais a
(primordial) é o produto dos números primos menores ou iguais a  . Assim, como exemplo, podemos tomar qualquer primo. Seja
. Assim, como exemplo, podemos tomar qualquer primo. Seja 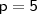 , daí,
, daí,
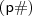 será um múltiplo de 3, com efeito,
será um múltiplo de 3, com efeito, 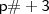 também será múltiplo de 3.
também será múltiplo de 3.