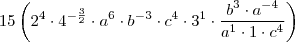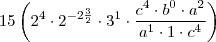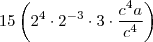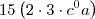por yuripa » Seg Ago 17, 2015 01:46
por yuripa » Seg Ago 17, 2015 01:46
Ola, estou tentando resolver essa questao da ufsc que basicamente envolve apenas conceitos de potencia. Eu consigo anular o B e o C, mas nunca consigo cortar o A completamente, e como a resposta se trata de um numero puro, devo estar fazendo algo muito errado.
Resposta = 90.
OBS: Nao da pra ver direito na imagem, mas o C mais da esquerda é elevado a 8/3.
- Anexos
-
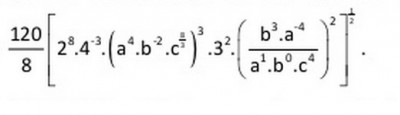
- UFSC
-
yuripa
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Ago 17, 2015 01:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Seg Ago 17, 2015 11:43
por nakagumahissao » Seg Ago 17, 2015 11:43
Editado pela última vez por
nakagumahissao em Ter Ago 18, 2015 03:13, em um total de 3 vezes.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por yuripa » Seg Ago 17, 2015 14:16
por yuripa » Seg Ago 17, 2015 14:16
Ola, primeiramente obrigado pela resposta.
Quando voce passou o 1/2 multiplicando, por que o a^2 que estava em baixo nao foi multiplicado tambem? Ele nao deveria ter virado a^1? O c^8 que estava do lado foi, e virou c^4, nao entendi por que o a nao foi.
-
yuripa
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Ago 17, 2015 01:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Ter Ago 18, 2015 03:15
por nakagumahissao » Ter Ago 18, 2015 03:15
Bem observado! Você têm razão.
Fiz as correções necessárias. Acredito que a resposta do gabarito esteja faltando este "a".
Obrigado
Sandro
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ufsc 2007
por manuoliveira » Seg Dez 13, 2010 21:45
- 2 Respostas
- 10964 Exibições
- Última mensagem por analauraa_b

Seg Mar 27, 2023 21:47
Geometria Plana
-
- Álgebra - UFSC
por thamaracm » Sáb Nov 10, 2012 06:44
- 1 Respostas
- 3282 Exibições
- Última mensagem por young_jedi

Sáb Nov 10, 2012 10:20
Álgebra Elementar
-
- Prisma ufsc 1996
 por Maria Livia » Sáb Nov 10, 2012 10:25
por Maria Livia » Sáb Nov 10, 2012 10:25
- 2 Respostas
- 12820 Exibições
- Última mensagem por Maria Livia

Sáb Nov 10, 2012 10:47
Geometria Espacial
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3682 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3761 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\frac{120}{8}\left[2^8\cdot 4^{-3} \cdot \left(a^{4} \cdot b^{-2} \cdot c^{\frac{8}{3}} \right)^{3} \cdot 3^2 \cdot \left(\frac{b^3 \cdot a^{-4}}{a^{1} \cdot b^{0} \cdot c^{4} \right)^{2}} \right]^{\frac{1}{2}} \frac{120}{8}\left[2^8\cdot 4^{-3} \cdot \left(a^{4} \cdot b^{-2} \cdot c^{\frac{8}{3}} \right)^{3} \cdot 3^2 \cdot \left(\frac{b^3 \cdot a^{-4}}{a^{1} \cdot b^{0} \cdot c^{4} \right)^{2}} \right]^{\frac{1}{2}}](/latexrender/pictures/fd789da8558a850e046e0373af180617.png)
![\frac{120}{8}\left[2^8\cdot 4^{-3} \cdot a^{12} \cdot b^{-6} \cdot c^{8} \cdot 3^2 \cdot \frac{b^6 \cdot a^{-8}}{a^{2} \cdot b^{0} \cdot c^{8}} \right]^{\frac{1}{2}} \frac{120}{8}\left[2^8\cdot 4^{-3} \cdot a^{12} \cdot b^{-6} \cdot c^{8} \cdot 3^2 \cdot \frac{b^6 \cdot a^{-8}}{a^{2} \cdot b^{0} \cdot c^{8}} \right]^{\frac{1}{2}}](/latexrender/pictures/912ff80746c34896d51e40463af1cf31.png)