 por ShadowOnLine » Sex Nov 07, 2014 22:12
por ShadowOnLine » Sex Nov 07, 2014 22:12
Bons dias, amigos. Eu recebi a seguinte questão, e gostaria que ela fosse avaliada, para saber se minha forma de pensar está correta.
QUESTÃO
Luiza, Sérgio e Ramon trabalham no mesmo colégio há 10, 8 e 4 anos, respectivamente.
O colégio distribuiu uma gratificação de R$ 6.600,00 para esses três funcionários em partes diretamente proporcionais ao tempo de serviço de cada um.
Quanto cada um receberá de gratificação?
Ora, eu pensei, se cada um receberá pelo tempo trabalhado, devo saber quanto da gratificação a ser distribuída vale um ano, e depois multiplicar este resultado pelo tempo de trabalho de cada uma das pessoas.
Então eu fiz 10 + 8 + 4 = 22 para saber em quantas partes a gratificação deverá ser divida.
Daí fiz 6600 / 22 = 300 que é o valor da gratificação por cada ano trabalhado.
Segui para a resposta:
Luiza receberá 300 * 10 = R$ 3.000,00
Sérgio receberá 300 * 8 = R$ 2.400,00
Ramon receberá 300 * 4 = R$ 1.200,00
Obrigado antecipado.
-
ShadowOnLine
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Abr 13, 2011 23:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Letras com Inglês
- Andamento: formado
 por ShadowOnLine » Sáb Nov 08, 2014 21:24
por ShadowOnLine » Sáb Nov 08, 2014 21:24
-
ShadowOnLine
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Abr 13, 2011 23:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Letras com Inglês
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- RAZÃO
por hevhoram » Qua Jun 02, 2010 11:50
- 1 Respostas
- 1535 Exibições
- Última mensagem por Molina

Qua Jun 02, 2010 18:43
Álgebra Elementar
-
- razao
por hevhoram » Qua Jun 02, 2010 20:14
- 2 Respostas
- 1678 Exibições
- Última mensagem por hevhoram

Qui Jun 03, 2010 20:42
Álgebra Elementar
-
- Razão
por Guaciara » Qui Set 23, 2010 22:40
- 2 Respostas
- 2407 Exibições
- Última mensagem por Guaciara

Qui Set 23, 2010 23:31
Conversão de Unidades
-
- razão
por angeloka » Sex Out 15, 2010 19:29
- 8 Respostas
- 6797 Exibições
- Última mensagem por MarceloFantini

Sáb Out 23, 2010 01:41
Álgebra Elementar
-
- PA com razão 0,3
por gustavowelp » Sex Nov 19, 2010 08:42
- 5 Respostas
- 3448 Exibições
- Última mensagem por 0 kelvin

Sex Nov 19, 2010 15:51
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


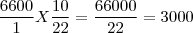
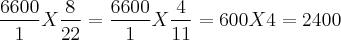
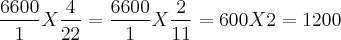


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.