a fração
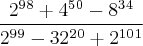 é igual a:
é igual a:R:
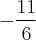
Eu consegui chegar até aqui
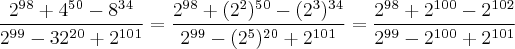


Russman escreveu:Fatore ono numerador e no denominador da fração.
![\[-\frac{12}{6}\] \[-\frac{12}{6}\]](/latexrender/pictures/9690d337a5e4522118adb92960c0d2a2.png)
![\[-\frac{11}{6}\] \[-\frac{11}{6}\]](/latexrender/pictures/4f15d97d803bcaf12871bbf3abd436b2.png)


![\[2^9^8+2^9^8.2^2-2^9^8.2^4 = 2^9^8(2^2-2^4) = -12\] \[2^9^8+2^9^8.2^2-2^9^8.2^4 = 2^9^8(2^2-2^4) = -12\]](/latexrender/pictures/b19ff1fbcff57dc14c378eee52ef226f.png)

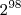 . Lembre-se que
. Lembre-se que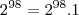

Russman escreveu:Você está esquecendo do. Lembre-se que
Daí, na fatoração, deve aparecer o 1 dentro do parenteses de soma.
![\[2^9^8.1+2^9^8.1.2^2.1-2^9^8.1.2^4.1\] \[2^9^8.1+2^9^8.1.2^2.1-2^9^8.1.2^4.1\]](/latexrender/pictures/8cd4e2299c6ee4532c72ff1aa15c26bd.png)

 real vale que
real vale que 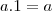 .
.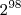 é real, então lhe vale também.
é real, então lhe vale também.
![\[2\] \[2\]](/latexrender/pictures/be925bb0484e70a9bb16de9234189f47.png) , para que o
, para que o ![\[2^9^8\] \[2^9^8\]](/latexrender/pictures/de11eeb00dd05abd2fb61002cc129e95.png) não ficasse solo, vc multiplicou ele por
não ficasse solo, vc multiplicou ele por ![\[1\] \[1\]](/latexrender/pictures/39519c38890a1efba600f88225f2eef8.png) ?
? ![\[2^9^8+2^9^8.2^2-2^9^8.2^4\] \[2^9^8+2^9^8.2^2-2^9^8.2^4\]](/latexrender/pictures/394d04ec3e59f588af4e00c0e4b85744.png) quase todos são multiplicados por
quase todos são multiplicados por ![\[2\] \[2\]](/latexrender/pictures/be925bb0484e70a9bb16de9234189f47.png) menos o primeiro
menos o primeiro ![\[2^9^8\] \[2^9^8\]](/latexrender/pictures/de11eeb00dd05abd2fb61002cc129e95.png) , e pra não deixar ele sozinho vc usou a propriedade
, e pra não deixar ele sozinho vc usou a propriedade ![\[a.1=a\] \[a.1=a\]](/latexrender/pictures/854349db0a8cc2ff2e88d1e454d22333.png)
![\[a.1=a\] \[a.1=a\]](/latexrender/pictures/854349db0a8cc2ff2e88d1e454d22333.png) para igualar?
para igualar?
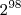 não é algo que façamos noção.
não é algo que façamos noção.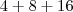 , certo? É claro que
, certo? É claro que 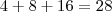 . Né? Ok. Mas, seguindo a sua lógica iríamos fatorar essa soma da seguinte forma:
. Né? Ok. Mas, seguindo a sua lógica iríamos fatorar essa soma da seguinte forma: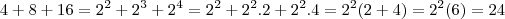
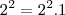 . Veja:
. Veja: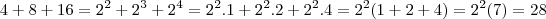



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)