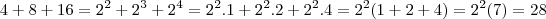por Bielto » Sex Mar 14, 2014 11:30
por Bielto » Sex Mar 14, 2014 11:30
bom dia!
a fração
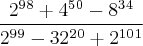
é igual a:
R: 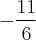
Eu consegui chegar até aqui
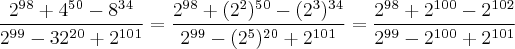
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Sex Mar 14, 2014 19:40
por Russman » Sex Mar 14, 2014 19:40
Fatore o
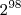
no numerador e no denominador da fração.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Sex Mar 14, 2014 20:02
por Bielto » Sex Mar 14, 2014 20:02
Russman escreveu:Fatore o
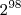
no numerador e no denominador da fração.
Boa noite,
Já fiz isso porem o meu resultado chegou no
![\[-\frac{12}{6}\] \[-\frac{12}{6}\]](/latexrender/pictures/9690d337a5e4522118adb92960c0d2a2.png)
e o gabarito é
![\[-\frac{11}{6}\] \[-\frac{11}{6}\]](/latexrender/pictures/4f15d97d803bcaf12871bbf3abd436b2.png)
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Sex Mar 14, 2014 22:47
por Russman » Sex Mar 14, 2014 22:47
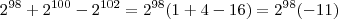
Por que você calculou -12?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Sex Mar 14, 2014 23:07
por Bielto » Sex Mar 14, 2014 23:07
Boa noite Russman
Cheguei seguinte,
![\[2^9^8+2^9^8.2^2-2^9^8.2^4 = 2^9^8(2^2-2^4) = -12\] \[2^9^8+2^9^8.2^2-2^9^8.2^4 = 2^9^8(2^2-2^4) = -12\]](/latexrender/pictures/b19ff1fbcff57dc14c378eee52ef226f.png)
Realmente não sei onde tem o 1 hehe...
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Sáb Mar 15, 2014 10:30
por Russman » Sáb Mar 15, 2014 10:30
Você está esquecendo do
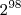
. Lembre-se que
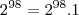
Daí, na fatoração, deve aparecer o 1 dentro do parenteses de soma.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Sáb Mar 15, 2014 13:46
por Bielto » Sáb Mar 15, 2014 13:46
Russman escreveu:Você está esquecendo do
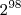
. Lembre-se que
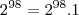
Daí, na fatoração, deve aparecer o 1 dentro do parenteses de soma.
Boa tarde Russman.
Não estou lembrado dessa propriedade da fatoração.
No caso, seria pra todos serem multiplicados por 1? Ex:
![\[2^9^8.1+2^9^8.1.2^2.1-2^9^8.1.2^4.1\] \[2^9^8.1+2^9^8.1.2^2.1-2^9^8.1.2^4.1\]](/latexrender/pictures/8cd4e2299c6ee4532c72ff1aa15c26bd.png)
Editado pela última vez por
Bielto em Sáb Mar 15, 2014 14:02, em um total de 1 vez.
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Sáb Mar 15, 2014 13:49
por Russman » Sáb Mar 15, 2014 13:49
Sim!
Lembre-se que o número 1 é o elemento neutro da multiplicação.
Para qualquer numero

real vale que
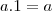
.
Como
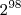
é real, então lhe vale também.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Sáb Mar 15, 2014 14:16
por Bielto » Sáb Mar 15, 2014 14:16
'
Deixa eu ver se entendi...
Como todos já possuíam seus multiplicadores por
![\[2\] \[2\]](/latexrender/pictures/be925bb0484e70a9bb16de9234189f47.png)
, para que o
![\[2^9^8\] \[2^9^8\]](/latexrender/pictures/de11eeb00dd05abd2fb61002cc129e95.png)
não ficasse solo, vc multiplicou ele por
![\[1\] \[1\]](/latexrender/pictures/39519c38890a1efba600f88225f2eef8.png)
?
Porque aqui
![\[2^9^8+2^9^8.2^2-2^9^8.2^4\] \[2^9^8+2^9^8.2^2-2^9^8.2^4\]](/latexrender/pictures/394d04ec3e59f588af4e00c0e4b85744.png)
quase todos são multiplicados por
![\[2\] \[2\]](/latexrender/pictures/be925bb0484e70a9bb16de9234189f47.png)
menos o primeiro
![\[2^9^8\] \[2^9^8\]](/latexrender/pictures/de11eeb00dd05abd2fb61002cc129e95.png)
, e pra não deixar ele sozinho vc usou a propriedade
![\[a.1=a\] \[a.1=a\]](/latexrender/pictures/854349db0a8cc2ff2e88d1e454d22333.png)
Faz sentido o que eu disse?
OBS: (Sempre que existir um exercício como esse ou até com letras, e o nº não tiver um multiplicador eu posso usar essa propriedade?
![\[a.1=a\] \[a.1=a\]](/latexrender/pictures/854349db0a8cc2ff2e88d1e454d22333.png)
para igualar?
vlw
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Sáb Mar 15, 2014 14:25
por Russman » Sáb Mar 15, 2014 14:25
Perfeito! Exatamente.
Tenho certeza que você concorda comigo, só não vê isto pq o número
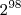
não é algo que façamos noção.
Pense comigo: Vamos efetuar a soma
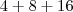
, certo? É claro que
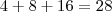
. Né? Ok. Mas, seguindo a sua lógica iríamos fatorar essa soma da seguinte forma:
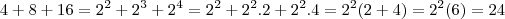
Está errado! Sim, pois você esqueceu de colocar o 1 de
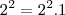
. Veja:
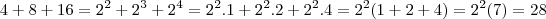
Parece pertinente, não?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bielto » Sáb Mar 15, 2014 14:29
por Bielto » Sáb Mar 15, 2014 14:29
Você é simplesmente foda, respondeu a minha pergunta com um exemplo, nada melhor do que isso.
Tu é bom cara.
Valeu mesmo, de verdade.
-
Bielto
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Qui Jul 12, 2012 15:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Médio
- Andamento: formado
 por Russman » Sáb Mar 15, 2014 14:38
por Russman » Sáb Mar 15, 2014 14:38
Obrigado! Fico feliz que tenha entendido.
Bons estudos!
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3769 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8604 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- Potenciação - Potência de potência
por Ana Paula MMS » Sáb Jan 11, 2014 14:59
- 1 Respostas
- 2631 Exibições
- Última mensagem por Cleyson007

Sáb Jan 11, 2014 17:27
Aritmética
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 2038 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
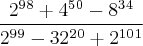 é igual a:
é igual a: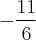
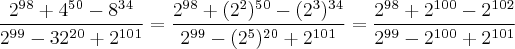


no numerador e no denominador da fração.
![\[-\frac{12}{6}\] \[-\frac{12}{6}\]](/latexrender/pictures/9690d337a5e4522118adb92960c0d2a2.png)
![\[-\frac{11}{6}\] \[-\frac{11}{6}\]](/latexrender/pictures/4f15d97d803bcaf12871bbf3abd436b2.png)


![\[2^9^8+2^9^8.2^2-2^9^8.2^4 = 2^9^8(2^2-2^4) = -12\] \[2^9^8+2^9^8.2^2-2^9^8.2^4 = 2^9^8(2^2-2^4) = -12\]](/latexrender/pictures/b19ff1fbcff57dc14c378eee52ef226f.png)

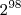 . Lembre-se que
. Lembre-se que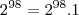

. Lembre-se que
![\[2^9^8.1+2^9^8.1.2^2.1-2^9^8.1.2^4.1\] \[2^9^8.1+2^9^8.1.2^2.1-2^9^8.1.2^4.1\]](/latexrender/pictures/8cd4e2299c6ee4532c72ff1aa15c26bd.png)

 real vale que
real vale que 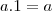 .
.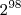 é real, então lhe vale também.
é real, então lhe vale também.
![\[2\] \[2\]](/latexrender/pictures/be925bb0484e70a9bb16de9234189f47.png) , para que o
, para que o ![\[2^9^8\] \[2^9^8\]](/latexrender/pictures/de11eeb00dd05abd2fb61002cc129e95.png) não ficasse solo, vc multiplicou ele por
não ficasse solo, vc multiplicou ele por ![\[1\] \[1\]](/latexrender/pictures/39519c38890a1efba600f88225f2eef8.png) ?
? ![\[2^9^8+2^9^8.2^2-2^9^8.2^4\] \[2^9^8+2^9^8.2^2-2^9^8.2^4\]](/latexrender/pictures/394d04ec3e59f588af4e00c0e4b85744.png) quase todos são multiplicados por
quase todos são multiplicados por ![\[2\] \[2\]](/latexrender/pictures/be925bb0484e70a9bb16de9234189f47.png) menos o primeiro
menos o primeiro ![\[2^9^8\] \[2^9^8\]](/latexrender/pictures/de11eeb00dd05abd2fb61002cc129e95.png) , e pra não deixar ele sozinho vc usou a propriedade
, e pra não deixar ele sozinho vc usou a propriedade ![\[a.1=a\] \[a.1=a\]](/latexrender/pictures/854349db0a8cc2ff2e88d1e454d22333.png)
![\[a.1=a\] \[a.1=a\]](/latexrender/pictures/854349db0a8cc2ff2e88d1e454d22333.png) para igualar?
para igualar?
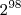 não é algo que façamos noção.
não é algo que façamos noção.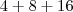 , certo? É claro que
, certo? É claro que 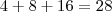 . Né? Ok. Mas, seguindo a sua lógica iríamos fatorar essa soma da seguinte forma:
. Né? Ok. Mas, seguindo a sua lógica iríamos fatorar essa soma da seguinte forma: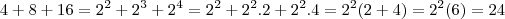
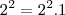 . Veja:
. Veja: