 por Sobreira » Sáb Out 05, 2013 16:34
por Sobreira » Sáb Out 05, 2013 16:34
Não estou conseguindo resolver esta questão abaixo (retirada de uma prova de concurso para engenheiro eletricista).
O enunciado fala que a equação matricial abaixo foi obtida através de uma análise de correntes de malha em um circuito, então a partir disso o exercício pede que seja calculada a potência total fornecida.

x

=

.
Resolvendo pela regra de Cramer encontrei I1 = 4 ampéres e I2 = 3,5 ampéres (Quanto à resolução por Cramer não tenho dúvidas).
Realizei a multiplicação de matrizes para tentar visualizar mais fácil o problema, mas não me ajudou muito:


A minha dúvida é:
Como que agora, a partir destas informações consigo determinar a potência fornecida ???
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Bravim » Sáb Out 05, 2013 21:04
por Bravim » Sáb Out 05, 2013 21:04
A minha solução seria diagonalizar :

Daqui fica fácil ver que

e
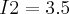
-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Sobreira » Sáb Out 05, 2013 21:40
por Sobreira » Sáb Out 05, 2013 21:40
Ok. Eu tinha esquecido de falar. Essas correntes eu já tinha calculado pela regra de Cramer mesmo.
Sei que tenho as tensões, as correntes, mas a partir daí para calcular a potência total fornecida não consigo chegar no valor.
A partir daí como você faria para chegar no valor da potência total dissipada ??
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Bravim » Sáb Out 05, 2013 22:23
por Bravim » Sáb Out 05, 2013 22:23
Bem, só com a corrente elétrica é impossível calcular a Potência dissipada. Você vai precisar usar a fórmula P=U*i e i=U/R com algum dado que a mais como a tensão ou a resistência elétrica.
-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Sobreira » Dom Out 06, 2013 13:00
por Sobreira » Dom Out 06, 2013 13:00
Então pessoal, consegui modelar o circuito a partir daquelas equações e aih está. Mas ainda há um problema, o exercício pede a potência total fornecida, o sentido das correntes estão corretos como pode ser visto nos amperímetros e conforme calculado anteriormente. Segundo a convenção passiva, se a corrente entrar pelo terminal negativo do elemento, este elemento estará fornecendo potência ao circuito, portanto a resposta seria 57.5 watts entretanto a resposta do gabarito é 22.5 Watts. E agora ???
- Anexos
-

- Circuito
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Circuito elétrico - Calcular a potência aparente total.
 por Sobreira » Qui Mai 01, 2014 18:41
por Sobreira » Qui Mai 01, 2014 18:41
- 0 Respostas
- 1438 Exibições
- Última mensagem por Sobreira

Qui Mai 01, 2014 18:41
Equações
-
- Circuito Elétrico
 por Rafael16 » Seg Mar 18, 2013 19:19
por Rafael16 » Seg Mar 18, 2013 19:19
- 1 Respostas
- 11760 Exibições
- Última mensagem por young_jedi

Seg Mar 18, 2013 20:43
Eletricidade I
-
- Circuito Elétrico sem solução.
 por Sobreira » Qui Set 19, 2013 02:20
por Sobreira » Qui Set 19, 2013 02:20
- 3 Respostas
- 7924 Exibições
- Última mensagem por young_jedi

Sáb Set 21, 2013 11:27
Aritmética
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3769 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 x
x  =
=  .
.




 e
e 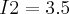




 , avisa que eu resolvo.
, avisa que eu resolvo.

