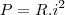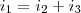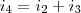Circuito Elétrico sem solução.

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Circuito Elétrico sem solução.

Regras do fórum
Responder

Circuito Elétrico sem solução.

Mensagempor Sobreira » Qui Set 19, 2013 02:20

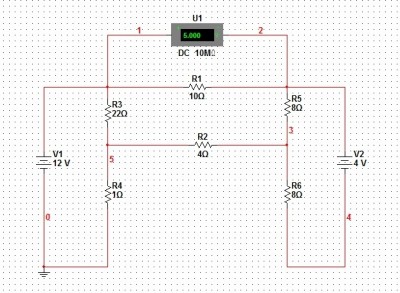
O exercício informa que a tensão sobre o resistor de 10 ohms é 5V e pede a potência dissipada no resistor de 4 ohms.
Já tentei algumas técnicas e não consegui resolver.
Anexos
Circuito2.jpg
"The good thing about science is that it's true whether or not you believe in it."
Sobreira
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 122
Registrado em: Sex Out 12, 2012 17:33
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Engenharia Elétrica
Andamento: formado
Voltar ao topo

Re: Circuito Elétrico sem solução.

Mensagempor young_jedi » Sex Set 20, 2013 18:51

sendo a tensão 5V e a resistência 10 ohms então a corrente que passa por ele é 0,5A

essa corrente também é igual a corrente que passa pelo resistor de 4 ohms pois esse é o único caminho que ela tem para retornar

portanto a potencia no resistor de 4 ohms sera

P=R.i^2

P=4.(0,5)^2=1 W
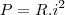
young_jedi
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1239
Registrado em: Dom Set 09, 2012 10:48
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica - UEL
Andamento: formado
Voltar ao topo

Re: Circuito Elétrico sem solução.

Mensagempor Sobreira » Sáb Set 21, 2013 00:09

Mas aí a corrente não se dividirá no nó acima do resistor R5 e/ou no nó acima de R6 ???
"The good thing about science is that it's true whether or not you believe in it."
Sobreira
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 122
Registrado em: Sex Out 12, 2012 17:33
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Engenharia Elétrica
Andamento: formado
Voltar ao topo

Re: Circuito Elétrico sem solução.

Mensagempor young_jedi » Sáb Set 21, 2013 11:27

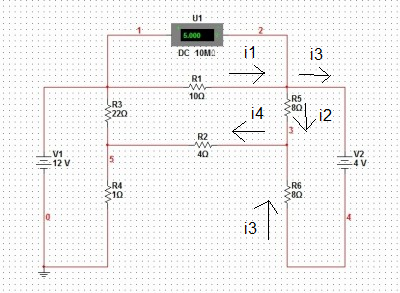
circuito.png
circuito.png (131.41 KiB) Exibido 7599 vezes


temos que

i_1=i_2+i_3

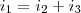
e

i_4=i_2+i_3

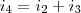
portanto

i_1=i_4

repare que ela se divide em um nó e depois se soma no outro
young_jedi
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1239
Registrado em: Dom Set 09, 2012 10:48
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica - UEL
Andamento: formado
Voltar ao topo
Responder

Voltar para Aritmética

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum