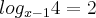 .
.Fiz o seguinte:
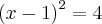
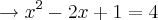
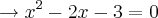 .
.Aplicando Bháskara:
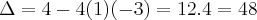
![\rightarrow {x}_{1}=\frac{2+\sqrt[2]{48}}{2}= \rightarrow {x}_{1}=\frac{2+\sqrt[2]{48}}{2}=](/latexrender/pictures/3bad29dee697b8b9f80f2c6ffc909663.png)
![\frac{2(1+2\sqrt[2]{3})}{2}=1+2\sqrt[2]{3} \frac{2(1+2\sqrt[2]{3})}{2}=1+2\sqrt[2]{3}](/latexrender/pictures/5cb9382d00271608fbb7f8cc579e2396.png) e
e ![{x}_{2}=1-2\sqrt[2]{3} {x}_{2}=1-2\sqrt[2]{3}](/latexrender/pictures/1c3d1ca56935cf58d683031cb0c46fc7.png) .
.Porém testando estes valores, não há como afirmar que estes valores para x estão corretos.
Outra maneira de fazer, que dá certo, é:
![{(x-1)}^{2}=4\rightarrow x-1=\sqrt[2]{4} {(x-1)}^{2}=4\rightarrow x-1=\sqrt[2]{4}](/latexrender/pictures/d09662607d18874c9dea136b8f5a7bd6.png)
Daí:
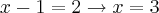
ou
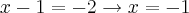
Logo, S={3}, pois x=-1 não satisfaz a condição de existência do logaritmo, tal que a base deve ser positiva e diferente de 1.
Eu gostaria de saber o motivo pelo qual a primeira resolução não funciona, ou qual é o erro nela.
Obrigada!


 errado.
errado.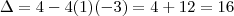
 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

