 por Lana » Ter Mai 07, 2013 16:47
por Lana » Ter Mai 07, 2013 16:47
(CEFET-2011)Um engenheiro tem R$ 1.942,00 para comprar os pisos de tipos A e B, sendo que o metro quadrado de A custa R$ 46,00 e o de B, R$ 32,00. Para encontrar as quantidades x e y , em metros quadrados, dos respectivos pisos, e gastar exatamente a quantia disponível, um matemático lhe propôs o seguinte enigma: “Para qualquer inteiro t ,há uma solução inteira, não necessariamente positiva, dada por:

e

.

=mdc(46,32)”.
Pode-se concluir, corretamente, que existe (m):
Gabarito:Somente duas soluções com valores positivos.
Não intendi o que seria esse t , e ao que devo iguala-lo.
-
Lana
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Abr 24, 2013 19:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Compução
- Andamento: cursando
 por Luis Gustavo » Ter Mai 07, 2013 18:32
por Luis Gustavo » Ter Mai 07, 2013 18:32
Temos
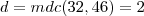
. Então:
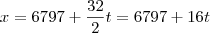
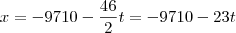
Estas fórmulas, para qualquer t inteiro que você inserir nelas, irão gerar valores de x e y que satisfarão o problema do engenheiro. Mas note que estes valores nem sempre serão positivos, e nós queremos apenas valores positivos (ou nulos, já que o engenheiro pode não comprar nenhum piso de determinado tipo), pois é impossível comprar um número negativo de pisos. Vamos então ver para quais valores de t teremos x positivo:
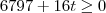

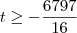
Note que
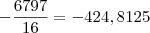
. Mas t deve ser inteiro, então vamos aproximar
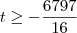
como

Agora vamos ver para que valores de t teremos y positivo:

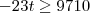

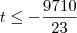
Temos
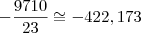
, motivo pelo qual mais uma vez vamos aproximar
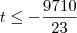
como

Vamos ver o que fizemos até aqui:
- Descobrimos que, para que x seja positivo, devemos ter

- Descobrimos que, para que y seja positivo, devemos ter

Mas precisamos que x e y sejam
ambos positivos, isto é, t deve pertencer aos dois intervalos ao mesmo tempo. Então, devemos ter
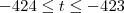
. Só existem dois valores possíveis para t nesse intervalo: t=-424 ou t =-423. Logo, são duas soluções com valores positivos. O problema não pede, mas as soluções são as listadas abaixo:
Se

do piso A e

do piso B.
Se

do piso A e
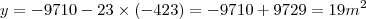
do piso B.
Resposta: Pode-se concluir, corretamente, que existem duas soluções com valores positivos:

e
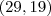
.
Conseguiu entender todo o raciocínio?
Espero ter ajudado.
Att, Luis Gustavo.
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Lana » Ter Mai 07, 2013 19:55
por Lana » Ter Mai 07, 2013 19:55
Perfeitamente.
Grato pela atenção.
Abraços
-
Lana
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Abr 24, 2013 19:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Compução
- Andamento: cursando
Voltar para Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  .
. =mdc(46,32)”.
=mdc(46,32)”.
 e
e  .
. =mdc(46,32)”.
=mdc(46,32)”.
. Então:
. Mas t deve ser inteiro, então vamos aproximar
como
, motivo pelo qual mais uma vez vamos aproximar
como
. Só existem dois valores possíveis para t nesse intervalo: t=-424 ou t =-423. Logo, são duas soluções com valores positivos. O problema não pede, mas as soluções são as listadas abaixo:
do piso A e
do piso B.
do piso A e
do piso B.
e
.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
