-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478696 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534700 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498287 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 713973 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2136053 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por DannN1 » Sáb Nov 26, 2016 11:16
por DannN1 » Sáb Nov 26, 2016 11:16
Seja E um conjunto não vazio e P(E)={x/xcE}.
Podemos definir operações em P(E).Dados X,Y pertence ao conjunto P(E).
XUYcE e X intersecção YcE.
Mostre que União e Intersecção são associativas e comutativas.
Boa tarde pessoal. Desculpem pela escrita.
Algo que eu sei sobre operação da associativa precisa de mais uma termo "Z" para aplicar a definição. Mas não sei como usá-lo.
Atenciosamente Danilo
-
DannN1
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Nov 26, 2016 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por adauto martins » Dom Nov 27, 2016 18:14
por adauto martins » Dom Nov 27, 2016 18:14
uniao:
propriedade associativa:dados

,teremos:
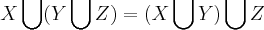
...para se provar uma igualdade em conj.teremos q. provar q.

,farei a ida...ou seja:

...logo,dado um elemento

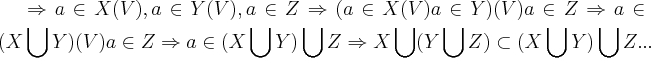
,onde
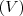
conectivo "ou",
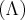
conectivo "e"...
comutatividade:
farei a comutatividade da intersecçao:

,dados
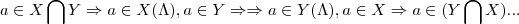
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes] Comutatividade .
por e8group » Ter Jul 10, 2012 22:16
- 3 Respostas
- 5470 Exibições
- Última mensagem por e8group

Sáb Jul 14, 2012 11:47
Matrizes e Determinantes
-
- ASSOCIATIVIDADE E COMUTATIVIDADE SOBRE R2
por EANDRIOLI » Seg Abr 23, 2012 02:02
- 0 Respostas
- 1340 Exibições
- Última mensagem por EANDRIOLI

Seg Abr 23, 2012 02:02
Álgebra Elementar
-
- operações de conjuntos
por Sergio Ribeiro Alves » Qui Fev 14, 2008 10:40
- 1 Respostas
- 3750 Exibições
- Última mensagem por admin

Qui Fev 14, 2008 16:21
Álgebra Elementar
-
- Matriz operações
por DanielRJ » Qui Set 09, 2010 18:06
- 5 Respostas
- 3369 Exibições
- Última mensagem por DanielRJ

Sex Set 10, 2010 17:15
Matrizes e Determinantes
-
- Operações com Conjuntos
por tertulia » Qui Dez 30, 2010 20:17
- 0 Respostas
- 1162 Exibições
- Última mensagem por tertulia

Qui Dez 30, 2010 20:17
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ,teremos:
,teremos: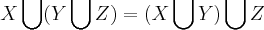 ...para se provar uma igualdade em conj.teremos q. provar q.
...para se provar uma igualdade em conj.teremos q. provar q. ,farei a ida...ou seja:
,farei a ida...ou seja: ...logo,dado um elemento
...logo,dado um elemento 
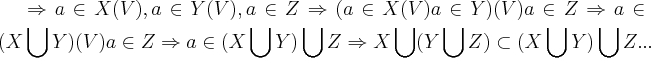 ,onde
,onde 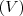 conectivo "ou",
conectivo "ou",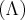 conectivo "e"...
conectivo "e"... ,dados
,dados 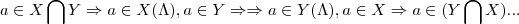


 .
.
 :
: