-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478191 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532029 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495567 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 706343 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2122691 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por adauto martins » Sex Jul 15, 2016 14:48
por adauto martins » Sex Jul 15, 2016 14:48
mostre que:
![({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})} ({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})}](/latexrender/pictures/976e752b1029475407a343e64b08f424.png)
,onde
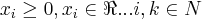
...
soluçao:
vamos tomar
![{A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}} {A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}}](/latexrender/pictures/a10c9338979f7c016248e98d37b8b432.png)
,segue q.:
![{A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})}) {A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})})](/latexrender/pictures/ff1ecfdb44b6842a944bc1e69d4b0fb4.png)
,prove isso!...tomaremos entao:
![({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})} ({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})}](/latexrender/pictures/cc25d6feb6f5966e58dd51262d6de7f7.png)
[Unparseable or potentially dangerous latex formula. Error 2 ]
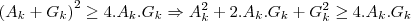
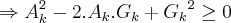
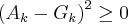
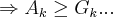
,pois se tomarmos
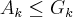
,contaria a condiçao de
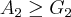
...logo,
![({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})} ({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})}](/latexrender/pictures/a23374e1a6641565b8e0038c12cfdb8e.png)
...cqd...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercicio resolvido
por adauto martins » Qua Jul 20, 2016 18:35
- 0 Respostas
- 14175 Exibições
- Última mensagem por adauto martins

Qua Jul 20, 2016 18:35
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Ter Jul 26, 2016 17:43
- 0 Respostas
- 6231 Exibições
- Última mensagem por adauto martins

Ter Jul 26, 2016 17:43
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Sáb Ago 13, 2016 11:28
- 0 Respostas
- 3833 Exibições
- Última mensagem por adauto martins

Sáb Ago 13, 2016 11:28
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Sex Out 18, 2019 14:29
- 2 Respostas
- 8381 Exibições
- Última mensagem por adauto martins

Sex Out 18, 2019 15:42
Trigonometria
-
- exercicio resolvido
por adauto martins » Sáb Out 19, 2019 21:12
- 2 Respostas
- 10047 Exibições
- Última mensagem por adauto martins

Sáb Out 19, 2019 23:51
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})} ({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})}](/latexrender/pictures/976e752b1029475407a343e64b08f424.png) ,onde
,onde 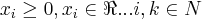 ...
...![{A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}} {A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}}](/latexrender/pictures/a10c9338979f7c016248e98d37b8b432.png) ,segue q.:
,segue q.:![{A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})}) {A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})})](/latexrender/pictures/ff1ecfdb44b6842a944bc1e69d4b0fb4.png) ,prove isso!...tomaremos entao:
,prove isso!...tomaremos entao:![({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})} ({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})}](/latexrender/pictures/cc25d6feb6f5966e58dd51262d6de7f7.png) [Unparseable or potentially dangerous latex formula. Error 2 ]
[Unparseable or potentially dangerous latex formula. Error 2 ]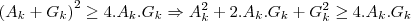
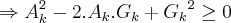
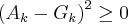
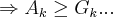 ,pois se tomarmos
,pois se tomarmos 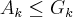 ,contaria a condiçao de
,contaria a condiçao de 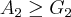 ...logo,
...logo,![({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})} ({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})}](/latexrender/pictures/a23374e1a6641565b8e0038c12cfdb8e.png) ...cqd...
...cqd...
![({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})} ({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})}](/latexrender/pictures/976e752b1029475407a343e64b08f424.png) ,onde
,onde 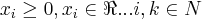 ...
...![{A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}} {A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}}](/latexrender/pictures/a10c9338979f7c016248e98d37b8b432.png) ,segue q.:
,segue q.:![{A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})}) {A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})})](/latexrender/pictures/ff1ecfdb44b6842a944bc1e69d4b0fb4.png) ,prove isso!...tomaremos entao:
,prove isso!...tomaremos entao:![({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})} ({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})}](/latexrender/pictures/cc25d6feb6f5966e58dd51262d6de7f7.png) [Unparseable or potentially dangerous latex formula. Error 2 ]
[Unparseable or potentially dangerous latex formula. Error 2 ]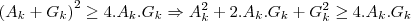
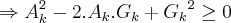
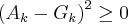
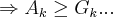 ,pois se tomarmos
,pois se tomarmos 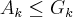 ,contaria a condiçao de
,contaria a condiçao de 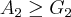 ...logo,
...logo,![({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})} ({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})}](/latexrender/pictures/a23374e1a6641565b8e0038c12cfdb8e.png) ...cqd...
...cqd...
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.