 por JessicaHayanne » Qui Mar 21, 2013 17:41
por JessicaHayanne » Qui Mar 21, 2013 17:41
Demonstrar que a²+b²+ab é maior ou igual a 0.
Consegui demonstrar utilizando a=0 e b=0; e também a>0 e b>0 porém o professor disse que ainda falta um passo e nao sei.
Por favor Ajudem.
Grata desde já.
Att.
Jéssica Hayanne
-
JessicaHayanne
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jun 20, 2012 13:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Qui Mar 21, 2013 19:17
por e8group » Qui Mar 21, 2013 19:17
Boa tarde ,vou propor algumas dicas .
(1)
Você provou que

para
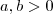
e

.
Sua demonstração está incompleta ,pois não considerou o caso em que
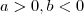
e

e ambos

.
(2) Segue outra resolução ,qualquer dúvida retorne !
Claramente para qualquer

real (verifique!) ,
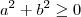
e ainda
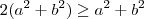
;logo
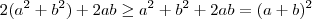
.
Ou seja ,

.
De
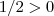
e
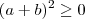
para qualquer real

,obtemos que
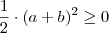
. Conclusão :
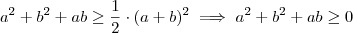
.
Espero que esteja correto .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Indução] Para todo n maior igual que 2
por +danile10 » Dom Fev 17, 2013 13:07
- 2 Respostas
- 1983 Exibições
- Última mensagem por e8group

Dom Fev 17, 2013 14:40
Lógica
-
- determinante igual a zero
 por dyegosouza_14dbte » Dom Mar 01, 2015 21:07
por dyegosouza_14dbte » Dom Mar 01, 2015 21:07
- 1 Respostas
- 7114 Exibições
- Última mensagem por Russman

Dom Mar 01, 2015 22:44
Matrizes e Determinantes
-
- Altura do trapézio igual ao diâmetro da circunferencia ?
por gustavoluiss » Ter Dez 14, 2010 07:12
- 1 Respostas
- 2228 Exibições
- Última mensagem por MarceloFantini

Ter Dez 14, 2010 13:49
Geometria Analítica
-
- Álgebra Elementar - Verificar se equação é igual
por johnlaw » Dom Fev 27, 2011 14:14
- 5 Respostas
- 3353 Exibições
- Última mensagem por Renato_RJ

Seg Fev 28, 2011 15:12
Álgebra Elementar
-
- Demonstrar que a função f é igual a uma certa série
por fff » Seg Jan 05, 2015 17:15
- 4 Respostas
- 4615 Exibições
- Última mensagem por fff

Qua Jan 07, 2015 18:14
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 para
para 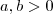 e
e  .
.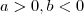 e
e  e ambos
e ambos  .
. real (verifique!) ,
real (verifique!) , 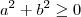 e ainda
e ainda 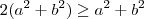 ;logo
;logo 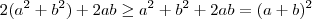 .
.  .
. 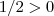 e
e 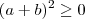 para qualquer real
para qualquer real  ,obtemos que
,obtemos que 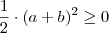 . Conclusão :
. Conclusão : 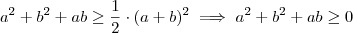 .
.