por Jhennyfer » Ter Jun 18, 2013 17:27
A afirmativa no gabarito está correta... mas alguém pode me explicar porque?!
- Toda dízima periódica provém da divisão de dois números inteiros, portanto é um número racional.
Boom, os números 0,1 e 0,9 não são números racionais??
se 0,1/0,9 resulta em uma dízima periódica 0,111...
então porque a afirmativa coloca somente números inteiros?
Obg desde já
-
Jhennyfer
- Usuário Parceiro
-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
por temujin » Ter Jun 18, 2013 18:11
Todo número racional é pode ser representado por uma razão entre dois inteiros. Neste caso que vc citou:
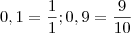
Logo, toda dízima é resultado da divisão de inteiros.
-
temujin
- Usuário Parceiro
-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
por Jhennyfer » Qua Jun 19, 2013 13:20
Bom... isso eu entendi!
Mas sinceramente, não fiquei conformada ainda... pois independente da origem, os números 0,1 e 0,9 propriamente ditos são racionais... e dividindo-os obteremos uma dízima!
Enfim... obrigado pela a explicação,
eu compreendi perfeitamente a linha de raciocínio.
-
Jhennyfer
- Usuário Parceiro
-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30
Então, o exercicio pede para encontrar
.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:
Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):
Somando a primeira e a segunda equação:
Finalmente:
Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
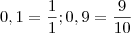
