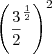
Pessoal como eu resolvo isso?
Please.
Desde já agradeço.

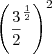

![{3}^{\frac{1}{2}}=\sqrt[]{3} {3}^{\frac{1}{2}}=\sqrt[]{3}](/latexrender/pictures/5d69480e12bfc9816db8282f773283c8.png)
![\left(\frac{\sqrt[]{3}}{2} \right)^2=\frac{3}{4} \left(\frac{\sqrt[]{3}}{2} \right)^2=\frac{3}{4}](/latexrender/pictures/29957a7d9dabcaaa2cf271548df8c4e8.png)


MarceloFantini escreveu:É só usar as propriedades quee
.

Cleyson007 escreveu:
Logo,

 ), que ao ser elevado por 2 temos
), que ao ser elevado por 2 temos 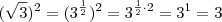 , enquanto que no denominador é só elevar,
, enquanto que no denominador é só elevar, 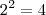 .
.

MarceloFantini escreveu:Não, aquelas propriedades não são derivada, muito longe disso.
A primeira propriedade diz que se temos uma fração elevada a um expoente, isto é a mesma coisa que a fração que tem o numerador elevado a esse expoente e o denominador também elevado ao mesmo expoente.
A segunda propriedade diz que quando temos um número elevado a um expoente, e você eleva tudo à outro expoente, o efeito que isso produz é multiplicar, e não somar, os expoentes.
O que o Cleyson fez foi aplicar ambas, como eu sugeri: no numerador, você já tem um expoente no numerador (), que ao ser elevado por 2 temos
, enquanto que no denominador é só elevar,
.

Voltar para Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

