por vagnerluiz » Sáb Jun 01, 2013 20:37
por vagnerluiz » Sáb Jun 01, 2013 20:37
como faço para resolver essa questao ?
120 pacotes de balas seriam distribuídos igualmente por certa quantidade de crianças de
uma comunidade. No momento da partilha, verificou-se que havia mais cinco crianças e,
desse modo, cada criança presente recebeu dois pacotes de balas a menos. Quantos pacotes
de balas recebeu cada criança?
-
vagnerluiz
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Jun 01, 2013 20:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Rafael16 » Sáb Jun 01, 2013 23:15
por Rafael16 » Sáb Jun 01, 2013 23:15
Boa noite
vagnerluiz!
vamos chamar de
x a quantidade de crianças, e
q a quantidade de pacotes que cada criança iria receber.
Então fica assim:
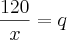
(I)
Mas na hora de distribuir os pacotes tinha 5 crianças a mais e, consequentemente, cada criança recebeu dois pacotes a menos (q-2):
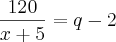
(II)
Isolando o x da equação I e substituindo na equação II, iremos encontrar a quantidade de pacotes que cada criança iria receber.

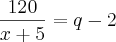

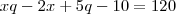

Desenvolvendo essa conta iremos chegar numa equação do segundo grau, em que q' = 8 e q''=-6. Não existe quantidade de pacotes negativos, então q = 8.
Como cada criança recebeu dois pacotes a menos, a quantidade recebida vai ser:
q - 2 = 8 - 2 = 6Qualquer dúvida comenta ai.
Abraço!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por vagnerluiz » Dom Jun 02, 2013 07:34
por vagnerluiz » Dom Jun 02, 2013 07:34
obrigado rafael
-
vagnerluiz
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Jun 01, 2013 20:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questao do Cesupa
por Paula Leite » Sex Nov 08, 2013 12:34
- 0 Respostas
- 3599 Exibições
- Última mensagem por Paula Leite

Sex Nov 08, 2013 12:34
Pedidos
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12984 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10964 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15106 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5018 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


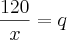 (I)
(I)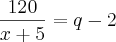 (II)
(II)