Boa noite
vagnerluiz!
vamos chamar de
x a quantidade de crianças, e
q a quantidade de pacotes que cada criança iria receber.
Então fica assim:
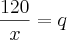
(I)
Mas na hora de distribuir os pacotes tinha 5 crianças a mais e, consequentemente, cada criança recebeu dois pacotes a menos (q-2):
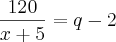
(II)
Isolando o x da equação I e substituindo na equação II, iremos encontrar a quantidade de pacotes que cada criança iria receber.

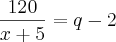

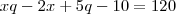

Desenvolvendo essa conta iremos chegar numa equação do segundo grau, em que q' = 8 e q''=-6. Não existe quantidade de pacotes negativos, então q = 8.
Como cada criança recebeu dois pacotes a menos, a quantidade recebida vai ser:
q - 2 = 8 - 2 = 6Qualquer dúvida comenta ai.
Abraço!


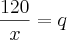 (I)
(I)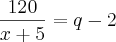 (II)
(II)

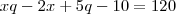




 , avisa que eu resolvo.
, avisa que eu resolvo.

