-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478038 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530680 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 494265 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 702539 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2115681 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por m0x0 » Sáb Jul 21, 2012 18:47
por m0x0 » Sáb Jul 21, 2012 18:47
Boa noite a todos,
Gostaria de saber, se possível, se estes exercícios que resolvi e entreguei a uma professora minha, merecem a nota que ela me deu.
Resolvi os exercícios com um colega meu e ele acabou por ter 16 valores e eu apenas tive 5 valores.
Não acho justo que, alguns professores, seja por falta de carácter, seja por terem embirrado connosco, nos possam dar uma nota destas.
Peço que apenas me digam se realmente a resolução destes exercícios merece a nota de 5 valores, porque tenho a noção do que fiz, e não penso que mereça menos de 12 ou 13 valores.
O comentário da professora foi o seguinte: "Infelizmente o seu trabalho não chega para passar. Com um trabalho de avaliação feito em casa, não se compreende que tenha errado nas definições."
Cada alínea vale 3 valores, excepto a 2 a), que vale 2 valores.
Obrigado.
http://imageshack.us/photo/my-images/843/99832567.jpg/http://imageshack.us/photo/my-images/821/20324985.jpg/http://imageshack.us/photo/my-images/411/32557063.jpg/http://imageshack.us/photo/my-images/694/73911528.jpg/
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jul 22, 2012 03:27
por MarceloFantini » Dom Jul 22, 2012 03:27
M0x0,seguindo as regras do fórum, por favor digite todos os enunciados e suas respectivas resoluções.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por m0x0 » Dom Jul 22, 2012 16:06
por m0x0 » Dom Jul 22, 2012 16:06
O Enunciado é:
1. Seja

um Espaço Vectorial e sejam

,

,

,

,

e u vectores de

.
a) Provar que se u? <

,

> e

,

? <

,

,

> então u ? <

,

,

>.
b) Se o sistema (

,

,

,

,

) é linearmente independente, o mesmo acontece com o sistema (

,

,

).
2. Sejam F e G subespaços vectoriais de um espaço vectorial

, provar que:
a) 0?F.
b) F?G é um subespaço vectorial de

.
3. Sejam

e

espaços vectoriais sobre o corpo K e ?:V?U uma aplicação linear. Mostrar que:
a) Se (

,…,

) é um sistema de vectores linearmente dependente, então o mesmo acontece com o sistema (?(

),…,?(

)).
b) Se F=<

,…,

>, então ?(F)=<?(

),…,?(

)>.
c) Se (

,…,

) é uma base de F e ? é injectiva, então (?(

),…,?(

)) é uma base de ?(F).
A minha resolução está feita nas imagens que fiz no primeiro post. Se for necessário eu faço aqui no latex.
Obrigado!
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jul 22, 2012 16:12
por MarceloFantini » Dom Jul 22, 2012 16:12
Por favor, escreva também suas resoluções. Facilita a busca no fórum depois.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por m0x0 » Dom Jul 22, 2012 20:15
por m0x0 » Dom Jul 22, 2012 20:15
Aqui vai a resolução do 1. a) e vou postar as outras:
1.
a) Sejam ?,?,

,

,

,

,
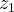
e
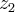
?K
E u ? <

,

>
Então existe pelo menos uma combinação linear de vectores de

e

tal que: u=?

+?

Analogamente, como

,

? <

,

,

>
Então existe pelo menos uma combinação linear de vectores de

,

e

tal que:

=


+


+
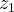


=


+


+
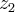

Logo
u=?

+?

=?(


+


+
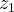

)+?(


+


+
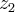

)
Pondo em evidência

,

e

obtemos:
u=

(?

+?

)+

(?

+?

)+

(?
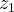
+?
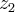
)
Como ?,?,

,

,

,

,
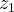
e
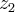
? K, logo:
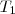
=?

+?

? K
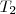
=?

+?

? K
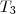
=?
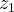
+?
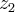
? K
E então u=
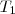

+
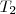

+
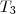

Logo u ? <

,

,

>
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por m0x0 » Seg Jul 23, 2012 15:20
por m0x0 » Seg Jul 23, 2012 15:20
1.
b) Sendo

,

,
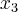
,

e

? K.
E como (

,

,

,

,

) é linearmente independente, por hipótese, isto quer dizer que:

+

+
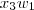
+

+
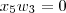
E que
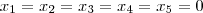
, ou seja, que a única combinação linear é a trivial.
Então:

<=>
<=>
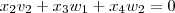
também é linearmente independente.
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por m0x0 » Seg Jul 23, 2012 15:29
por m0x0 » Seg Jul 23, 2012 15:29
2.
a) Como

é um espaço vectorial, por hipótese, então

?0 porque vai conter pelo menos o elemento nulo
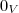
.
Como F?

então F?0 porque contém, pelo menos, um vector v?F tal que:

v?F?V,

?K
Em particular, fazendo v=0, temos que:
?0?F=>0?F
b) Sendo x,y ? (F?G) e ?,? ? K
Logo x,y ? F e também x,y ? G
Como, por hipótese, temos que F,G?

, então:
(?x+?y) ? F?

e também (?x+?y) ? G?

Então:
(?x+?y) ? (F?G)?

-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por m0x0 » Seg Jul 23, 2012 15:50
por m0x0 » Seg Jul 23, 2012 15:50
3.
a) Como, por hipótese, (

,…,

) é linearmente dependente,
Então


+?+


=0 não é a única combinação linear, ou seja, existe pelo menos mais uma combinação linear que não seja a trivial,
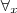
?K.
Como ? é uma aplicação linear, então:

?(

)+?+

?(

)=0
?(


)+?+(


)=0
?(


+?+


)=0
Como a aplicação linear perserva sempre o vector nulo, temos que:
?(


+?+


)=0 sse


+...+


=0
E como é linearmente dependente, existe pelo menos uma combinação linear nula que não seja a trivial, portanto (?(

),…,?(

)) também é linearmente dependente.
b) Como F=<

,…,

> então
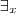
?F tal que:
x=


+?+


Como ?(F)=<?(

),…,?(

)>, então
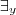
??(F) tal que:
y=

?(

),…,

?(

)
Então y??(F) sse y=?(x), com x?F.
Como ?(x)=?(


+?+


) e ? é uma aplicação linear, então:
?(


+?+


)=?(


)+?+?(


)=

?(

)+?+

?(

)
Ou seja, qualquer vector de ?(F) pode ser escrito como combinação linear dos vectores (?(

),…,?(

))
c) Sendo, por hipótese, (

,…,

) uma base de F, então:
F=<

,…,

> e (

,…,

) é linearmente independente.
Logo,
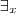
?F tal que:
x=


+?+


=0 é a única combinação linear – a trivial – porque (

,…,

) é linearmente independente.
Sendo ? injectiva, temos que a objectos distintos, correspondem imagens distintas, ou seja:
Se

???

então ?(

)????(

)
Seja então y= ?(F), então y= ?(x), com x?F.
Então y=?(


+?+


) e como ? é uma aplicação linear, logo:
y=?(


+?+


)= ?(


)+?+?(


)=

?(

)+?+

?(

)
Portanto ?(F)=<?(

),…,?(

)>
Como x=


+?+


=0 é linearmente independente, então:


+?+


=0 sse

=?=

=v
Logo:

?(

)+?+

?(

)=0
E como ? é uma aplicação linear:
?(


)+?+?(


)=0
?(


+?+


)=0
Logo (?(

),…,?(

)) é uma base de ?(F)
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Jul 24, 2012 00:31
por MarceloFantini » Ter Jul 24, 2012 00:31
Vamos lá. Primeiramente, dada uma base, todo vetor é combinação
única da base. Para ver isso, suponha que
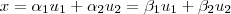
, com

. Então
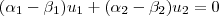
mas os coeficientes são não-nulos e assim

não seria base.
1)a) Seja
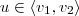
. Então existem coeficientes

tais que

. Como
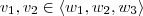
, então

. Mas daí

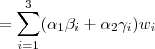
,
mostrando que
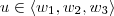
.
1)b) Como
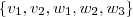
é linearmente independente, então vale a condição

Em particular,
 2)a)
2)a) Você errou logo no começo. Se

então

também é um espaço vetorial, cujo único elemento é o elemento neutro. Se

são subspaços vetoriais de

, então toda combinação linear de elementos de

permanecem nos respectivos espaços. Isto inclui a combinação nula, logo

.
2)b) Como fez está correto.
3)a) Se os vetores

são linearmente dependentes, então existem constantes

nem todas nulas, tais que

. Usando a aplicação linear nesta combinação, temos

,
ou seja, existe uma combinação linear dos vetores

igual a zero sendo que nem todos os coeficientes são nulos, portanto é linearmente dependente.
3)b) Seja

, então
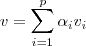
. Daí,
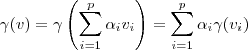
e assim

. Como
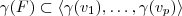
, segue
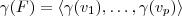
.
Seu erro neste item foi justamente assumir que
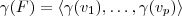
. É isto que você quer provar, é sua tese, não sua hipótese. Afirmando esta igualdade, não há nada para provar; se é o espaço gerado, é óbvio que qualquer vetor é escrito como combinação linear destes.
3)c) Seja
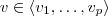
com
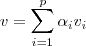
. Temos que

Como a aplicação linear

é injetiva, então segue que
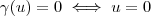
. Aplicando nesta combinação, temos
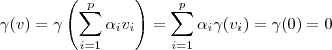
.
Pela injetividade, sabemos que

e disso
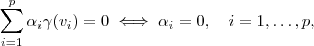
mostrando que o conjunto de vetores

é linearmente independente, portanto uma base de
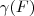
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por m0x0 » Ter Jul 24, 2012 08:31
por m0x0 » Ter Jul 24, 2012 08:31
Bom dia,
MarceloFantini, se fosses professor e olhando para as minhas resoluções, achas que mereço a nota de 5 valores? Tenho a noção que há alguns erros mas mesmo assim...
Todas as alinhas valem 3 valores, excepto a 2. a), que vale 2 valores.
Ainda por mais, não faltei a uma única aula, entreguei todos os trabalhos que a professora enviou para casa (que nunca chegou a corrigir nem a falar deles) e era suposto trata-se de avaliação contínua.
Obrigado!
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 2460 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- Algebra Linear para resolução de Conjutos
por SuPr3MeMoTF » Qui Out 15, 2015 17:11
- 1 Respostas
- 1741 Exibições
- Última mensagem por adauto martins

Qui Out 15, 2015 19:11
Álgebra Linear
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 7554 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 9788 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 8634 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 um Espaço Vectorial e sejam
um Espaço Vectorial e sejam  ,
,  ,
,  ,
,  ,
,  e u vectores de
e u vectores de  espaços vectoriais sobre o corpo K e ?:V?U uma aplicação linear. Mostrar que:
espaços vectoriais sobre o corpo K e ?:V?U uma aplicação linear. Mostrar que: ) é um sistema de vectores linearmente dependente, então o mesmo acontece com o sistema (?(
) é um sistema de vectores linearmente dependente, então o mesmo acontece com o sistema (?( ,
, ,
, ,
, ,
,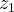 e
e 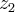 ?K
?K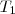 =?
=?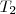 =?
=?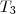 =?
=?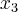 ,
, e
e  ? K.
? K. +
+ +
+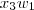 +
+ +
+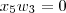
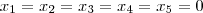 , ou seja, que a única combinação linear é a trivial.
, ou seja, que a única combinação linear é a trivial. <=>
<=> 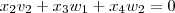 também é linearmente independente.
também é linearmente independente.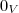 .
. v?F?V,
v?F?V, ?K
?K
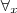 ?K.
?K.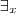 ?F tal que:
?F tal que: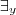 ??(F) tal que:
??(F) tal que: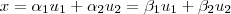 , com
, com  . Então
. Então 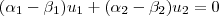 mas os coeficientes são não-nulos e assim
mas os coeficientes são não-nulos e assim  não seria base.
não seria base.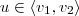 . Então existem coeficientes
. Então existem coeficientes  tais que
tais que  . Como
. Como 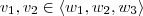 , então
, então  . Mas daí
. Mas daí
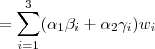 ,
,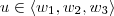 .
.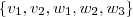 é linearmente independente, então vale a condição
é linearmente independente, então vale a condição 

 então
então  também é um espaço vetorial, cujo único elemento é o elemento neutro. Se
também é um espaço vetorial, cujo único elemento é o elemento neutro. Se  são subspaços vetoriais de
são subspaços vetoriais de  .
. são linearmente dependentes, então existem constantes
são linearmente dependentes, então existem constantes  nem todas nulas, tais que
nem todas nulas, tais que  . Usando a aplicação linear nesta combinação, temos
. Usando a aplicação linear nesta combinação, temos ,
, igual a zero sendo que nem todos os coeficientes são nulos, portanto é linearmente dependente.
igual a zero sendo que nem todos os coeficientes são nulos, portanto é linearmente dependente. , então
, então 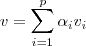 . Daí,
. Daí, 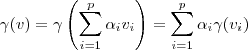
 . Como
. Como 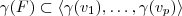 , segue
, segue 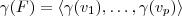 .
.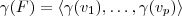 . É isto que você quer provar, é sua tese, não sua hipótese. Afirmando esta igualdade, não há nada para provar; se é o espaço gerado, é óbvio que qualquer vetor é escrito como combinação linear destes.
. É isto que você quer provar, é sua tese, não sua hipótese. Afirmando esta igualdade, não há nada para provar; se é o espaço gerado, é óbvio que qualquer vetor é escrito como combinação linear destes.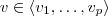 com
com 
 é injetiva, então segue que
é injetiva, então segue que 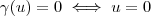 . Aplicando nesta combinação, temos
. Aplicando nesta combinação, temos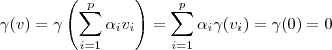 .
. e disso
e disso 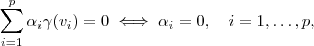 mostrando que o conjunto de vetores
mostrando que o conjunto de vetores 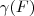 .
.

 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
