-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477931 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529911 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493486 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 700263 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2111678 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por m0x0 » Sáb Jul 21, 2012 18:47
por m0x0 » Sáb Jul 21, 2012 18:47
Boa noite a todos,
Gostaria de saber, se possível, se estes exercícios que resolvi e entreguei a uma professora minha, merecem a nota que ela me deu.
Resolvi os exercícios com um colega meu e ele acabou por ter 16 valores e eu apenas tive 5 valores.
Não acho justo que, alguns professores, seja por falta de carácter, seja por terem embirrado connosco, nos possam dar uma nota destas.
Peço que apenas me digam se realmente a resolução destes exercícios merece a nota de 5 valores, porque tenho a noção do que fiz, e não penso que mereça menos de 12 ou 13 valores.
O comentário da professora foi o seguinte: "Infelizmente o seu trabalho não chega para passar. Com um trabalho de avaliação feito em casa, não se compreende que tenha errado nas definições."
Cada alínea vale 3 valores, excepto a 2 a), que vale 2 valores.
Obrigado.
http://imageshack.us/photo/my-images/843/99832567.jpg/http://imageshack.us/photo/my-images/821/20324985.jpg/http://imageshack.us/photo/my-images/411/32557063.jpg/http://imageshack.us/photo/my-images/694/73911528.jpg/
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jul 22, 2012 03:27
por MarceloFantini » Dom Jul 22, 2012 03:27
M0x0,seguindo as regras do fórum, por favor digite todos os enunciados e suas respectivas resoluções.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por m0x0 » Dom Jul 22, 2012 16:06
por m0x0 » Dom Jul 22, 2012 16:06
O Enunciado é:
1. Seja

um Espaço Vectorial e sejam

,

,

,

,

e u vectores de

.
a) Provar que se u? <

,

> e

,

? <

,

,

> então u ? <

,

,

>.
b) Se o sistema (

,

,

,

,

) é linearmente independente, o mesmo acontece com o sistema (

,

,

).
2. Sejam F e G subespaços vectoriais de um espaço vectorial

, provar que:
a) 0?F.
b) F?G é um subespaço vectorial de

.
3. Sejam

e

espaços vectoriais sobre o corpo K e ?:V?U uma aplicação linear. Mostrar que:
a) Se (

,…,

) é um sistema de vectores linearmente dependente, então o mesmo acontece com o sistema (?(

),…,?(

)).
b) Se F=<

,…,

>, então ?(F)=<?(

),…,?(

)>.
c) Se (

,…,

) é uma base de F e ? é injectiva, então (?(

),…,?(

)) é uma base de ?(F).
A minha resolução está feita nas imagens que fiz no primeiro post. Se for necessário eu faço aqui no latex.
Obrigado!
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jul 22, 2012 16:12
por MarceloFantini » Dom Jul 22, 2012 16:12
Por favor, escreva também suas resoluções. Facilita a busca no fórum depois.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por m0x0 » Dom Jul 22, 2012 20:15
por m0x0 » Dom Jul 22, 2012 20:15
Aqui vai a resolução do 1. a) e vou postar as outras:
1.
a) Sejam ?,?,

,

,

,

,
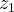
e
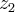
?K
E u ? <

,

>
Então existe pelo menos uma combinação linear de vectores de

e

tal que: u=?

+?

Analogamente, como

,

? <

,

,

>
Então existe pelo menos uma combinação linear de vectores de

,

e

tal que:

=


+


+
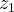


=


+


+
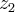

Logo
u=?

+?

=?(


+


+
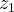

)+?(


+


+
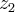

)
Pondo em evidência

,

e

obtemos:
u=

(?

+?

)+

(?

+?

)+

(?
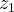
+?
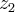
)
Como ?,?,

,

,

,

,
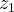
e
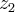
? K, logo:
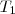
=?

+?

? K
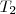
=?

+?

? K
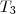
=?
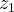
+?
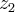
? K
E então u=
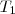

+
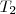

+
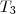

Logo u ? <

,

,

>
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por m0x0 » Seg Jul 23, 2012 15:20
por m0x0 » Seg Jul 23, 2012 15:20
1.
b) Sendo

,

,
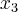
,

e

? K.
E como (

,

,

,

,

) é linearmente independente, por hipótese, isto quer dizer que:

+

+
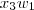
+

+
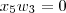
E que
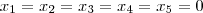
, ou seja, que a única combinação linear é a trivial.
Então:

<=>
<=>
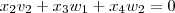
também é linearmente independente.
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por m0x0 » Seg Jul 23, 2012 15:29
por m0x0 » Seg Jul 23, 2012 15:29
2.
a) Como

é um espaço vectorial, por hipótese, então

?0 porque vai conter pelo menos o elemento nulo
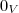
.
Como F?

então F?0 porque contém, pelo menos, um vector v?F tal que:

v?F?V,

?K
Em particular, fazendo v=0, temos que:
?0?F=>0?F
b) Sendo x,y ? (F?G) e ?,? ? K
Logo x,y ? F e também x,y ? G
Como, por hipótese, temos que F,G?

, então:
(?x+?y) ? F?

e também (?x+?y) ? G?

Então:
(?x+?y) ? (F?G)?

-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por m0x0 » Seg Jul 23, 2012 15:50
por m0x0 » Seg Jul 23, 2012 15:50
3.
a) Como, por hipótese, (

,…,

) é linearmente dependente,
Então


+?+


=0 não é a única combinação linear, ou seja, existe pelo menos mais uma combinação linear que não seja a trivial,
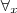
?K.
Como ? é uma aplicação linear, então:

?(

)+?+

?(

)=0
?(


)+?+(


)=0
?(


+?+


)=0
Como a aplicação linear perserva sempre o vector nulo, temos que:
?(


+?+


)=0 sse


+...+


=0
E como é linearmente dependente, existe pelo menos uma combinação linear nula que não seja a trivial, portanto (?(

),…,?(

)) também é linearmente dependente.
b) Como F=<

,…,

> então
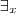
?F tal que:
x=


+?+


Como ?(F)=<?(

),…,?(

)>, então
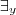
??(F) tal que:
y=

?(

),…,

?(

)
Então y??(F) sse y=?(x), com x?F.
Como ?(x)=?(


+?+


) e ? é uma aplicação linear, então:
?(


+?+


)=?(


)+?+?(


)=

?(

)+?+

?(

)
Ou seja, qualquer vector de ?(F) pode ser escrito como combinação linear dos vectores (?(

),…,?(

))
c) Sendo, por hipótese, (

,…,

) uma base de F, então:
F=<

,…,

> e (

,…,

) é linearmente independente.
Logo,
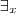
?F tal que:
x=


+?+


=0 é a única combinação linear – a trivial – porque (

,…,

) é linearmente independente.
Sendo ? injectiva, temos que a objectos distintos, correspondem imagens distintas, ou seja:
Se

???

então ?(

)????(

)
Seja então y= ?(F), então y= ?(x), com x?F.
Então y=?(


+?+


) e como ? é uma aplicação linear, logo:
y=?(


+?+


)= ?(


)+?+?(


)=

?(

)+?+

?(

)
Portanto ?(F)=<?(

),…,?(

)>
Como x=


+?+


=0 é linearmente independente, então:


+?+


=0 sse

=?=

=v
Logo:

?(

)+?+

?(

)=0
E como ? é uma aplicação linear:
?(


)+?+?(


)=0
?(


+?+


)=0
Logo (?(

),…,?(

)) é uma base de ?(F)
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Jul 24, 2012 00:31
por MarceloFantini » Ter Jul 24, 2012 00:31
Vamos lá. Primeiramente, dada uma base, todo vetor é combinação
única da base. Para ver isso, suponha que
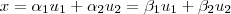
, com

. Então
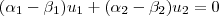
mas os coeficientes são não-nulos e assim

não seria base.
1)a) Seja
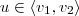
. Então existem coeficientes

tais que

. Como
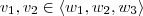
, então

. Mas daí

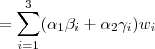
,
mostrando que
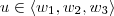
.
1)b) Como
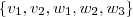
é linearmente independente, então vale a condição

Em particular,
 2)a)
2)a) Você errou logo no começo. Se

então

também é um espaço vetorial, cujo único elemento é o elemento neutro. Se

são subspaços vetoriais de

, então toda combinação linear de elementos de

permanecem nos respectivos espaços. Isto inclui a combinação nula, logo

.
2)b) Como fez está correto.
3)a) Se os vetores

são linearmente dependentes, então existem constantes

nem todas nulas, tais que

. Usando a aplicação linear nesta combinação, temos

,
ou seja, existe uma combinação linear dos vetores

igual a zero sendo que nem todos os coeficientes são nulos, portanto é linearmente dependente.
3)b) Seja

, então
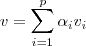
. Daí,
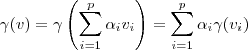
e assim

. Como
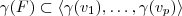
, segue
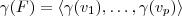
.
Seu erro neste item foi justamente assumir que
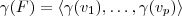
. É isto que você quer provar, é sua tese, não sua hipótese. Afirmando esta igualdade, não há nada para provar; se é o espaço gerado, é óbvio que qualquer vetor é escrito como combinação linear destes.
3)c) Seja
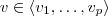
com
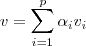
. Temos que

Como a aplicação linear

é injetiva, então segue que
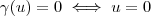
. Aplicando nesta combinação, temos
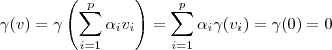
.
Pela injetividade, sabemos que

e disso
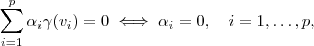
mostrando que o conjunto de vetores

é linearmente independente, portanto uma base de
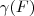
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por m0x0 » Ter Jul 24, 2012 08:31
por m0x0 » Ter Jul 24, 2012 08:31
Bom dia,
MarceloFantini, se fosses professor e olhando para as minhas resoluções, achas que mereço a nota de 5 valores? Tenho a noção que há alguns erros mas mesmo assim...
Todas as alinhas valem 3 valores, excepto a 2. a), que vale 2 valores.
Ainda por mais, não faltei a uma única aula, entreguei todos os trabalhos que a professora enviou para casa (que nunca chegou a corrigir nem a falar deles) e era suposto trata-se de avaliação contínua.
Obrigado!
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 2455 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- Algebra Linear para resolução de Conjutos
por SuPr3MeMoTF » Qui Out 15, 2015 17:11
- 1 Respostas
- 1740 Exibições
- Última mensagem por adauto martins

Qui Out 15, 2015 19:11
Álgebra Linear
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 7552 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 9780 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 8621 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 um Espaço Vectorial e sejam
um Espaço Vectorial e sejam  ,
,  ,
,  ,
,  ,
,  e u vectores de
e u vectores de  espaços vectoriais sobre o corpo K e ?:V?U uma aplicação linear. Mostrar que:
espaços vectoriais sobre o corpo K e ?:V?U uma aplicação linear. Mostrar que: ) é um sistema de vectores linearmente dependente, então o mesmo acontece com o sistema (?(
) é um sistema de vectores linearmente dependente, então o mesmo acontece com o sistema (?( ,
, ,
, ,
, ,
,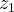 e
e 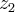 ?K
?K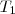 =?
=?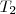 =?
=?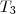 =?
=?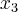 ,
, e
e  ? K.
? K. +
+ +
+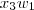 +
+ +
+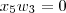
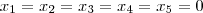 , ou seja, que a única combinação linear é a trivial.
, ou seja, que a única combinação linear é a trivial. <=>
<=> 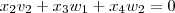 também é linearmente independente.
também é linearmente independente.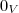 .
. v?F?V,
v?F?V, ?K
?K
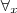 ?K.
?K.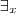 ?F tal que:
?F tal que: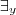 ??(F) tal que:
??(F) tal que: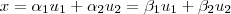 , com
, com  . Então
. Então 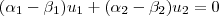 mas os coeficientes são não-nulos e assim
mas os coeficientes são não-nulos e assim  não seria base.
não seria base.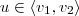 . Então existem coeficientes
. Então existem coeficientes  tais que
tais que  . Como
. Como 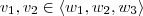 , então
, então  . Mas daí
. Mas daí
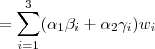 ,
,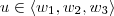 .
.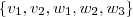 é linearmente independente, então vale a condição
é linearmente independente, então vale a condição 

 então
então  também é um espaço vetorial, cujo único elemento é o elemento neutro. Se
também é um espaço vetorial, cujo único elemento é o elemento neutro. Se  são subspaços vetoriais de
são subspaços vetoriais de  .
. são linearmente dependentes, então existem constantes
são linearmente dependentes, então existem constantes  nem todas nulas, tais que
nem todas nulas, tais que  . Usando a aplicação linear nesta combinação, temos
. Usando a aplicação linear nesta combinação, temos ,
, igual a zero sendo que nem todos os coeficientes são nulos, portanto é linearmente dependente.
igual a zero sendo que nem todos os coeficientes são nulos, portanto é linearmente dependente. , então
, então 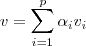 . Daí,
. Daí, 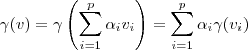
 . Como
. Como 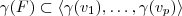 , segue
, segue 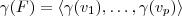 .
.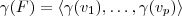 . É isto que você quer provar, é sua tese, não sua hipótese. Afirmando esta igualdade, não há nada para provar; se é o espaço gerado, é óbvio que qualquer vetor é escrito como combinação linear destes.
. É isto que você quer provar, é sua tese, não sua hipótese. Afirmando esta igualdade, não há nada para provar; se é o espaço gerado, é óbvio que qualquer vetor é escrito como combinação linear destes.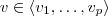 com
com 
 é injetiva, então segue que
é injetiva, então segue que 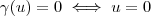 . Aplicando nesta combinação, temos
. Aplicando nesta combinação, temos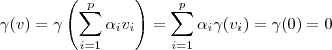 .
. e disso
e disso 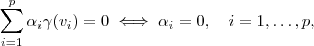 mostrando que o conjunto de vetores
mostrando que o conjunto de vetores 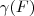 .
.