Pessoal,
Não estou conseguindo resolver a questão abaixo:
O espaço vetorial formado pelos pontos (x1, x2, x3, x4, x5, x6) do R6 tais que x1 = 0 e x5 + x6 = 0 tem dimensão:
(a) = 01
(b) = 02
(c) = 03
(d) = 04
(e) = 05
Está questão foi aplicada no último concurso do PROMINP e a resposta da mesma foi letra D.
Já procurei na teoria de álgebra as propriedades dos vetores e espaços vetorias, mas não consigo encontrar nada relacionado a dimensão.
Alguem poderia me ajudar?
Agradeço desde já.
João Campos




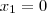 e
e  (ou seja,
(ou seja, 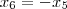 ), todos os vetores do espaço em questão tem o seguinte formato:
), todos os vetores do espaço em questão tem o seguinte formato: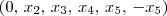
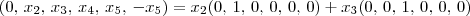

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)