 por douglasdizaro » Seg Nov 28, 2016 12:15
por douglasdizaro » Seg Nov 28, 2016 12:15
ESTOU COM UMA DUVIDA EM UM TRABALHO E GOSTARIA DE AJUDA!
16) Sejam V um espaço vetorial de dimensão igual a 6, U e W subespaços de V tais que:
a)dim(U) = 4 e dim(W) =5. Mostre que U interseção W é diferente de zero .
b)dim(U) = dim(w) = 4 . Encontre as possíveis dimensões para U interseção W .
-
douglasdizaro
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Nov 28, 2016 12:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por adauto martins » Ter Nov 29, 2016 09:28
por adauto martins » Ter Nov 29, 2016 09:28
a)
temos que:
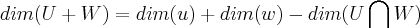
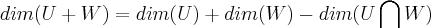
...
se
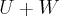
nao é soma direta,pois ai teriamos
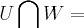
{0}
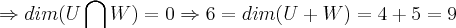
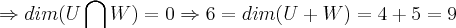
,logo nao pode ser soma direta...entao:
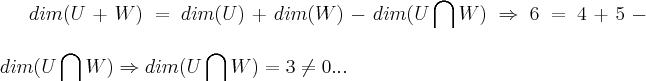
...
b)
se
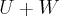
é soma direta,teriamos como visto anteriormente
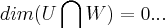
se
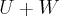
nao for soma direta,entao:
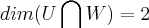
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8153 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10527 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11559 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13600 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9140 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


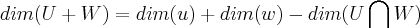
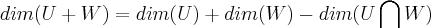 ...
... nao é soma direta,pois ai teriamos
nao é soma direta,pois ai teriamos  {0}
{0}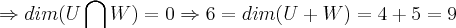
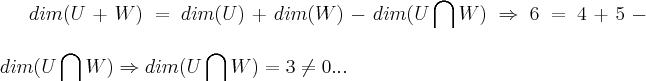 ...
...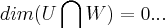
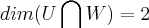 ...
...

 .
.



