 por bebelo32 » Seg Dez 01, 2014 19:31
por bebelo32 » Seg Dez 01, 2014 19:31
1)Para cada transformação linear abaixo determine o núcleo e a imagem
a) T :
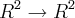
,T(x,y) = 2(x,y);
-
bebelo32
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mai 03, 2014 19:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: computação
- Andamento: formado
 por adauto martins » Ter Dez 02, 2014 16:25
por adauto martins » Ter Dez 02, 2014 16:25
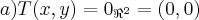
...

...logo N(T)={(0,0)=

}
B)
![T(x,y)=2(x,y)=2x(1,0)+2y(0,1)\Rightarrow {B}_{{\Re}^{2}}=[(1,0),(0,1)] T(x,y)=2(x,y)=2x(1,0)+2y(0,1)\Rightarrow {B}_{{\Re}^{2}}=[(1,0),(0,1)]](/latexrender/pictures/981a31731c9372f8392bd1049d0605d4.png)
,como

gera qquer subespaço de
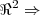
IM(T)={[1,0),(0,1)]=
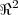
}
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Transformações e Espaços Lineares
por bebelo32 » Seg Dez 01, 2014 16:07
- 1 Respostas
- 987 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:23
Álgebra Linear
-
- Transformações e Espaços Lineares
por bebelo32 » Dom Dez 07, 2014 10:30
- 1 Respostas
- 1148 Exibições
- Última mensagem por adauto martins

Seg Dez 08, 2014 14:09
Álgebra Linear
-
- Transformações e Espaços Lineares
por bebelo32 » Seg Dez 08, 2014 17:32
- 0 Respostas
- 1125 Exibições
- Última mensagem por bebelo32

Seg Dez 08, 2014 17:32
Álgebra Linear
-
- Transformações e Espaços Lineares
por bebelo32 » Seg Mar 16, 2015 22:45
- 0 Respostas
- 1054 Exibições
- Última mensagem por bebelo32

Seg Mar 16, 2015 22:45
Álgebra Linear
-
- Transformações e Espaços Lineares
por bebelo32 » Ter Mar 17, 2015 11:48
- 1 Respostas
- 1949 Exibições
- Última mensagem por adauto martins

Sex Mar 20, 2015 12:26
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
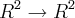 ,T(x,y) = 2(x,y);
,T(x,y) = 2(x,y);
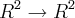 ,T(x,y) = 2(x,y);
,T(x,y) = 2(x,y);
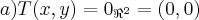 ...
... ...logo N(T)={(0,0)=
...logo N(T)={(0,0)= }
}![T(x,y)=2(x,y)=2x(1,0)+2y(0,1)\Rightarrow {B}_{{\Re}^{2}}=[(1,0),(0,1)] T(x,y)=2(x,y)=2x(1,0)+2y(0,1)\Rightarrow {B}_{{\Re}^{2}}=[(1,0),(0,1)]](/latexrender/pictures/981a31731c9372f8392bd1049d0605d4.png) ,como
,como  gera qquer subespaço de
gera qquer subespaço de 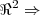 IM(T)={[1,0),(0,1)]=
IM(T)={[1,0),(0,1)]= }
}

 .
.
 :
: