[Representação Matricial] Op. linear definido por rotação

por **12200633** » Dom Jun 01, 2014 19:17

O enunciado é o seguinte:
Encontre a representação matricial canônica para cada um dos operadores lineares L em R² descritos a seguir:

a)L reflete cada vetor x em relação ao eixo dos x_1

e depois roda o vetor refletido de 90° no sentido trigonométrico.

Bem, eu pensei em fazer dessa forma: colocar cada um dos vetores da base canônica no plano cartesiano, realizar as operações de rotação solicitadas e assim descobrir o que a transformação faz com cada um dos vetores.

L(1, 0) = <reflete em relação ao eixo x> (-1, 0) <rodar o vetor refletido de 90° no sentido trigonométrico> bem o sentido trigonométrico que eu saiba é o anti horário, então rotacionando esse vetor fica (0, -1)

L(0, 1) = <reflete em relação ao eixo x> (0, -1) <rotar o vetor refletido de 90° no sentido trigonométrico> (1, 0)

assim: L(1, 0) = (0, -1), L(0, 1) = (-1, 0).

L(1, 0) = (0, -1) = 0*(1, 0) + (-1)*(0, 1)
L(0, 1) = (1, 0) = 1*(1, 0) + 0(0, 1)

assim a matriz de L fica: $\begin{pmatrix} 0 & 1 \\ -1 & 0\end{pmatrix}$

eu achava que é assim, porém existe outro exercício que é assim:
b) L dobra o comprimento de x e depois roda o vetor obtido de 30°no sentido trigonométrico.

aí eu acho que é com senos e cossenos e aí travei nessa parte, alguém pode me ajudar aí? a prova é amanhã hahaha D:

por **ant_dii** » Seg Jun 02, 2014 05:28

Verifique sua resposta do primeiro! Como você quer refletir em relação ao eixo

, o vetor

continua

. Se fosse outro vetor, digamos (a,b)

, refletido em relação ao eixo

ficaria

. A Transformação Linear neste caso, em geral, é dada por: L'(x,y) = (x,-y)

.

Quanto a rotação (daí ajuda nos dois problemas) a Transformação Linear, em geral, é dada por: $L''(x,y)=(x \cos \theta - y \sin \theta , x\sin \theta + y \cos \theta)$ , onde $\theta$ é o ângulo em que deseja fazer a rotação.

Lembre-se que o comprimento de um vetor v=(a,b)

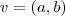é dado por: 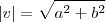$|v|=\sqrt{a^{2}+b^{2}}$ . Como você obtém o dobro desse comprimento?
Essa transformação será um caso particular das Homotetias (Semelhanças) dadas, em geral, por: L'''(x,y)=k(x,y)

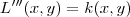, onde

é uma constante.

Para o segundo caso, se não quiser usar a fórmula, você pode raciocinar como fez no primeiro caso, mas tomando o cuidado de dobrar o comprimento do vetor e de usar triângulos retângulos para saber onde o novo ponto será projetado nos eixos (isso serve para encontrar as coordenadas).

Tente novamente e qualquer coisa retorne. Você esta no caminho certo.

[Representação Matricial] Op. linear definido por rotação

[Representação Matricial] Op. linear definido por rotação

[Representação Matricial] Op. linear definido por rotação

Re: [Representação Matricial] Op. linear definido por rotaçã

Quem está online