Obrigado Renato_RJ, entendi bem o procedimento. Foram somados dois elementos arbitrários de S, e com a própria condição do conjunto, p(0)=2p(1), foi possível verificar que a soma é bem definida.
Gostaria de entender melhor a ideia, para isso preciso saber se o seguinte raciocínio está correto:
Supondo que fosse dado um conjunto e pede-se para provar que é um
espaço vetorial, tomemos como exemplo o conjunto:

. Ora, mas seja
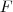
o conjunto das funções de R em R, sabemos que
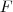
é um espaço vetorial, e de fato isso é simples de se provar, e como
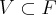
os elementos de V satisfazem as propriedades para espaço vetorial, logo para mostrar que V é um espaço, basta verificar se o vetor nulo e o simétrico estão em V, ou ainda verificar se a adição e a multiplicação por escalar estão bem definidas, o que recairia num procedimento análogo ao da questão anterior. Está certa essa conclusão?
Por outro lado, se for realmente necessário testar cada uma das oito propriedades de espaço, teria como realizar um procedimento semelhante ao do exercício anterior? Por exemplo, como provar a comutatividade na adição?
 .
.

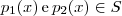 , então
, então
 um escalar e
um escalar e 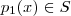 , então
, então

 . Ora, mas seja
. Ora, mas seja 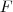 o conjunto das funções de R em R, sabemos que
o conjunto das funções de R em R, sabemos que 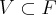 os elementos de V satisfazem as propriedades para espaço vetorial, logo para mostrar que V é um espaço, basta verificar se o vetor nulo e o simétrico estão em V, ou ainda verificar se a adição e a multiplicação por escalar estão bem definidas, o que recairia num procedimento análogo ao da questão anterior. Está certa essa conclusão?
os elementos de V satisfazem as propriedades para espaço vetorial, logo para mostrar que V é um espaço, basta verificar se o vetor nulo e o simétrico estão em V, ou ainda verificar se a adição e a multiplicação por escalar estão bem definidas, o que recairia num procedimento análogo ao da questão anterior. Está certa essa conclusão?

 , avisa que eu resolvo.
, avisa que eu resolvo.

