Olá pessoal, venho com mais algumas dúvidas sobre o incrível universo da álgebra linear. Bem, como não tenho a quem recorrer no fim de semana, são vocês que sempre salvam minha pele. Então, eis os problemas...
Determine se são subespaços vetoriais de F(R,R):
a) O conjunto das funções continuas;
b){f(x) = asen(x)+2, a pertence a R};
c){f(x)=ax²+b, b, a pertencem a R};
gab: Sim, não, sim
Tenho algumas deduções quanto a isso, mas não sei como provar, portanto, não sei se estou certo... Enfim, peço para que, por gentileza, se puderem me explicar do porque as respostas, ficarei grato.
Abraços!


 das funções contínuas ,de fato é um subespaço vetorial de.Pois ,
das funções contínuas ,de fato é um subespaço vetorial de.Pois , 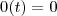 identicamente nula
identicamente nula 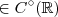 .
.  funções contínuas .Então :
funções contínuas .Então : 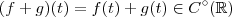 .
. 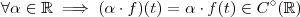
 não é subespaço vetorial de
não é subespaço vetorial de  .Pois ,tomando-se
.Pois ,tomando-se  (que é um número real) temos que não existe uma função identicamente nula neste conjunto ,não satisfazendo então uma propriedade do subespaço vetorial .
(que é um número real) temos que não existe uma função identicamente nula neste conjunto ,não satisfazendo então uma propriedade do subespaço vetorial . 
 não se exprime como
não se exprime como  independente da escolha do número
independente da escolha do número  .Se tivéssemos
.Se tivéssemos  ,então resultaria ,
,então resultaria ,  .Em particular para
.Em particular para  teríamos
teríamos  por outro lado
por outro lado  .
. tal que
tal que 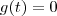 para todo
para todo  em
em  . Nossa tarefa seria mostrar então que
. Nossa tarefa seria mostrar então que 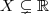 . Esta é uma outra forma também no meu ponto de vista .
. Esta é uma outra forma também no meu ponto de vista . em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.