Meu professor falou que tem que aparecer
 na inversa, mas eu não acho.
na inversa, mas eu não acho.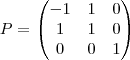

 na inversa, mas eu não acho.
na inversa, mas eu não acho.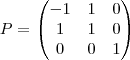

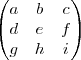 a matriz inversa de P.
a matriz inversa de P. 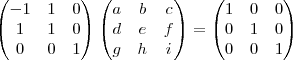





 se aplicando uma sequência
se aplicando uma sequência  de operações elementares em A chega-se em
de operações elementares em A chega-se em  então A é equivalente por linhas a matriz identidade .
então A é equivalente por linhas a matriz identidade .  .
.![[A|I_n] [A|I_n]](/latexrender/pictures/92869bfc9701c745591033e1a3446d3e.png)
![[I_n | E ] [I_n | E ]](/latexrender/pictures/634da1cc61ef7f61940fb7229089c4bd.png) ; a matriz
; a matriz  denomina-se inversa de
denomina-se inversa de  .
. 

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
