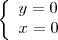T(x,y,z) = (x,y,z)

(1,1,1)
T(x,y,z) = (y-z , z-x , x-y)
T(x,y,z) = (0, -x, x) + (y, 0, -y) + (-z, z, 0)
T(x,y,z) = x(0, -1, 1) + y(1, 0, -1) + z(-1, 1, 0)
Ou seja, Im(T) é o conjunto gerado pelos vetores (0, -1, 1), (1, 0, -1) e (-1, 1, 0).
Opções:
(1) se os vetores são L.I., então Im(T) =

;
(2) se os vetores são L.D., então Im(T) forma algum plano ou alguma reta;
x(0, -1, 1) + y(1, 0, -1) + z(-1, 1, 0) = (0, 0, 0)

x = z = y que é diferente da solução trivial, então os vetores são linearmente dependentes. Descartando um deles, podemos dizer que
Im(T) é o conjunto gerado pelos vetores (0, -1, 1) e (1, 0, -1).
Opções:
(1) se os vetores são L.I., então Im(T) forma um plano;
(2) se os vetores são L.D., então Im(T) forma uma reta;
x(0, -1, 1) + y(1, 0, -1) = (0, 0, 0)
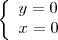
Que é a solução trivial. Logo os vetores são Linearmente independentes e Im(T) forma um plano.
Comparando aos planos dados nas alternativas, o único que se ajusta aos vetores (0, -1, 1) e (1, 0, -1), que são bases da Im(T), é x+y+z=0.
Logo, a resposta é a
alternativa D.
 (1,1,1), em que
(1,1,1), em que  indica o produto vetorial em
indica o produto vetorial em  , é:
, é:
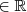
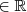

 (1,1,1), em que
(1,1,1), em que  indica o produto vetorial em
indica o produto vetorial em  , é:
, é:
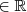
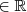

 (1,1,1)
(1,1,1) ;
;