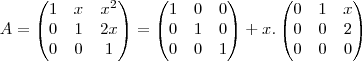por hyge » Qua Mai 02, 2018 17:04
por hyge » Qua Mai 02, 2018 17:04
Seja, para x ? R, a matriz A(x) dada por:
[list=]
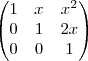
[/list]
a) Mostre que A(x+y) = A(x)*A(y), para x e y quaisquer.
b) Calcular o subespaço F de

(R), gerado pelo subconjunto {A(x), x ? R}. Pode explicitar F dando as equações que descrevem F ou
um sistema de geradores.
Nessa questão eu resolvi a letra A, no entanto, não estou conseguindo resolver a letra B. Não estou entendendo direito a pergunta e não to sabendo o passo inicial, gostaria que alguém me ajudasse, obrigado.
-
hyge
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Mai 02, 2018 16:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Dom Mai 06, 2018 12:24
por adauto martins » Dom Mai 06, 2018 12:24
b)

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Mai 06, 2018 12:28
por adauto martins » Dom Mai 06, 2018 12:28
ou mesmo:
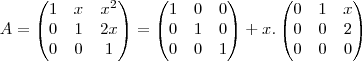
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Subespaço Vetorial] Verificar que é o conjunto é subespaço
por anderson_wallace » Seg Dez 30, 2013 17:56
- 3 Respostas
- 4676 Exibições
- Última mensagem por Renato_RJ

Ter Dez 31, 2013 14:00
Álgebra Linear
-
- subespaço vetorial
 por leobcastro » Seg Jun 16, 2008 10:18
por leobcastro » Seg Jun 16, 2008 10:18
- 8 Respostas
- 26963 Exibições
- Última mensagem por Heidji

Qua Jan 27, 2010 23:16
Geometria Analítica
-
- Subespaço vetorial
por drakonifor » Qui Mar 17, 2011 16:48
- 3 Respostas
- 3976 Exibições
- Última mensagem por LuizAquino

Qui Mar 17, 2011 18:39
Geometria Analítica
-
- subespaço vetorial
por amr » Seg Abr 18, 2011 10:56
- 3 Respostas
- 5235 Exibições
- Última mensagem por LuizAquino

Seg Abr 18, 2011 19:48
Introdução à Álgebra Linear
-
- Subespaço Vetorial.
por Jokeras » Qui Jun 30, 2011 22:53
- 0 Respostas
- 3651 Exibições
- Última mensagem por Jokeras

Qui Jun 30, 2011 22:53
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
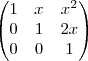 [/list]
[/list] (R), gerado pelo subconjunto {A(x), x ? R}. Pode explicitar F dando as equações que descrevem F ou
(R), gerado pelo subconjunto {A(x), x ? R}. Pode explicitar F dando as equações que descrevem F ou