 por adauto martins » Seg Ago 08, 2016 11:48
por adauto martins » Seg Ago 08, 2016 11:48
seja
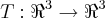
,definida por:
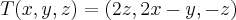
,determine:
a)uma base para o nucleo,e uma base para a imagem de

b)

é injetiva?

é sobrejetiva?
soluçao:
a)
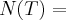
{
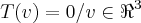
},logo:
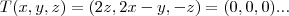
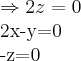

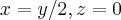
,logo
![v=(x,y,z)=(y/2,y,0)=y(1/2,1,0)\Rightarrow [N(T)]=[(1/2,1,0)] v=(x,y,z)=(y/2,y,0)=y(1/2,1,0)\Rightarrow [N(T)]=[(1/2,1,0)]](/latexrender/pictures/4fb25f42b64c7ffd9e3d345c5eddb225.png)
...

{
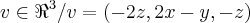
},entao
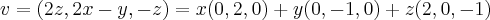
,como
![x(0,2,0),y(0,-1,0) sao LD (porque?)\Rightarrow [IM(T)]=[(0,2,0),(2,0-1)] x(0,2,0),y(0,-1,0) sao LD (porque?)\Rightarrow [IM(T)]=[(0,2,0),(2,0-1)]](/latexrender/pictures/77d3bf28f564922f238a6fe1918766d0.png)
ou
![[IM(T)]=[(0,-1,0),(2,0-1)]... [IM(T)]=[(0,-1,0),(2,0-1)]...](/latexrender/pictures/d7d2e395ecd79f1ea300b94965c35110.png)
...
b)

nao é injetiva,pois
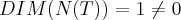
...

nao é sobrejetiva,pois
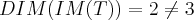
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
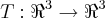 ,definida por:
,definida por: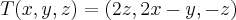 ,determine:
,determine:
 é injetiva?
é injetiva? é sobrejetiva?
é sobrejetiva?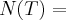 {
{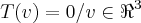 },logo:
},logo: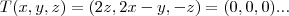
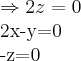

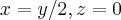 ,logo
,logo![v=(x,y,z)=(y/2,y,0)=y(1/2,1,0)\Rightarrow [N(T)]=[(1/2,1,0)] v=(x,y,z)=(y/2,y,0)=y(1/2,1,0)\Rightarrow [N(T)]=[(1/2,1,0)]](/latexrender/pictures/4fb25f42b64c7ffd9e3d345c5eddb225.png) ...
... {
{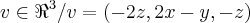 },entao
},entao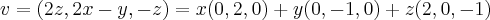 ,como
,como ![x(0,2,0),y(0,-1,0) sao LD (porque?)\Rightarrow [IM(T)]=[(0,2,0),(2,0-1)] x(0,2,0),y(0,-1,0) sao LD (porque?)\Rightarrow [IM(T)]=[(0,2,0),(2,0-1)]](/latexrender/pictures/77d3bf28f564922f238a6fe1918766d0.png)
![[IM(T)]=[(0,-1,0),(2,0-1)]... [IM(T)]=[(0,-1,0),(2,0-1)]...](/latexrender/pictures/d7d2e395ecd79f1ea300b94965c35110.png) ...
... nao é injetiva,pois
nao é injetiva,pois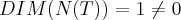 ...
... nao é sobrejetiva,pois
nao é sobrejetiva,pois 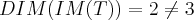 ...
...
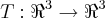 ,definida por:
,definida por: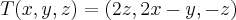 ,determine:
,determine:
 é injetiva?
é injetiva? é sobrejetiva?
é sobrejetiva?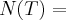 {
{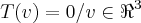 },logo:
},logo: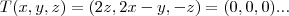
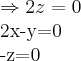

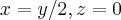 ,logo
,logo![v=(x,y,z)=(y/2,y,0)=y(1/2,1,0)\Rightarrow [N(T)]=[(1/2,1,0)] v=(x,y,z)=(y/2,y,0)=y(1/2,1,0)\Rightarrow [N(T)]=[(1/2,1,0)]](/latexrender/pictures/4fb25f42b64c7ffd9e3d345c5eddb225.png) ...
... {
{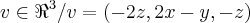 },entao
},entao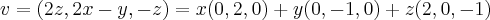 ,como
,como ![x(0,2,0),y(0,-1,0) sao LD (porque?)\Rightarrow [IM(T)]=[(0,2,0),(2,0-1)] x(0,2,0),y(0,-1,0) sao LD (porque?)\Rightarrow [IM(T)]=[(0,2,0),(2,0-1)]](/latexrender/pictures/77d3bf28f564922f238a6fe1918766d0.png)
![[IM(T)]=[(0,-1,0),(2,0-1)]... [IM(T)]=[(0,-1,0),(2,0-1)]...](/latexrender/pictures/d7d2e395ecd79f1ea300b94965c35110.png) ...
... nao é injetiva,pois
nao é injetiva,pois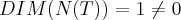 ...
... nao é sobrejetiva,pois
nao é sobrejetiva,pois 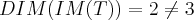 ...
...

 .
.
 :
: