Para destacar a importância de trabalhar com sistemas de equações não lineares, vamos levantar a situação em que existe a necessidade de realizar a análise do comportamento de um regime permanente do circuito não linear, quando os valores de tensão através dos resistores podem ser obtidos através da resolução de um sistema de equações não lineares, e o problema se reduz a encontrar uma raiz para o sistema de equações. Uma segunda situação permite mencionar que, no sistema aéreo, os controladores de voo trabalham com radares e, quando dois destes radares estão localizados em posições conhecidas, eles podem determinar a distância de suas localizações até uma aeronave que está se aproximando dentro do espaço aéreo. Neste caso, também temos um sistema de equações não lineares, e a solução está em calcular o valor das raízes das equações. Assim, efetue os seguintes cálculos:
Dado o sistema de equações não lineares:
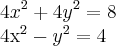
faça uma análise do sistema e, na sequência, assinale a alternativa CORRETA:
a - As derivadas parciais das duas funções que compõem o sistema apresentam ponto de descontinuidade.
b - No sistema, as variáveis x e y assumem o mesmo valor.
c - O Método de Newton é apropriado para calcular o erro relativo das variáveis com referência às raízes de ambas as funções.
d - As duas funções que compõem o sistema apresentam ponto de descontinuidade.
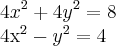


![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png) )/5,
)/5,![\sqrt[2]{6}/5 \sqrt[2]{6}/5](/latexrender/pictures/202e3a5ca87f6f4427bc85d3e4dc377c.png) ),(-
),(-![2(\sqrt[2]{5})/5 2(\sqrt[2]{5})/5](/latexrender/pictures/90f58da7be80c4fa3706a892c4d24ae8.png) ,
,![(\sqrt[2]{6})/5 (\sqrt[2]{6})/5](/latexrender/pictures/3dc979df27ad17edb4e4971d74ee2aa0.png) ),
),![-2(\sqrt[2]{5})/5 -2(\sqrt[2]{5})/5](/latexrender/pictures/1ce777c581640a126179528f89096b4b.png) ,
,![-(\sqrt[2]{6})/5 -(\sqrt[2]{6})/5](/latexrender/pictures/15c2774ba51a36b690a11272f33170e4.png) ),(
),(
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.