 por Knoner » Dom Set 29, 2013 19:49
por Knoner » Dom Set 29, 2013 19:49
Olá, estou em duvida na seguinte questão:
Sejam A, B, e Mn (R) e a £ R, mostre que:
a)(A^t)^t = A
b)(

A)^t =

A^t, onde

? K
c)Se n=m, (A.B)^t = B^T . A^T
-
Knoner
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Set 26, 2013 20:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Fisica
- Andamento: cursando
 por e8group » Seg Set 30, 2013 21:52
por e8group » Seg Set 30, 2013 21:52
Item a ) Utilizando a notação
![[A]_{ij} = a_{ij} [A]_{ij} = a_{ij}](/latexrender/pictures/696f564a2df9d77962db1d56d1f617c8.png)
para designar o termo geral da matriz e lembrando da definição de transposição de matrizes :
![[A^t]_{ij} = [A]_{ji} = a_{ji} [A^t]_{ij} = [A]_{ji} = a_{ji}](/latexrender/pictures/bb4429fd8d2c473fce86883ea5eeeef3.png)
(**) , temos que
![[(A^t)^t]_{ij} = [A^t]_{ji} = [A]_{ij} = a_{ij} [(A^t)^t]_{ij} = [A^t]_{ji} = [A]_{ij} = a_{ij}](/latexrender/pictures/a968c7178a1e4963ea162d4561724979.png)
para todo
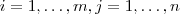
o que mostra

. No item b , utilize a definição (**) + propriedades dos números reais ,se não conseguir post . No item c , basta intercambiar a definição (**) juntamente com a definição produto de matrizes . Veja minha sugestão ,
![[(AB)^t]_{ij} = [AB]_{ji} = \sum_{k=1}^n a_{jk} \cdot b_{ki} [(AB)^t]_{ij} = [AB]_{ji} = \sum_{k=1}^n a_{jk} \cdot b_{ki}](/latexrender/pictures/164a9a91760a9c2213b4421a97d2384f.png)
. Sendo o produto
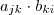
comutativo (pois ,

são números reais) e utilizando resultado do item (a) ,
![a_{jk} = [A^t]_{kj} , b_{kj} = [B^t]_{jk} a_{jk} = [A^t]_{kj} , b_{kj} = [B^t]_{jk}](/latexrender/pictures/bcc05bba66e675b80521c5cf67d26370.png)
. Seguindo estas dicas conseguirá concluir o exercício .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes] Dúvida .
por e8group » Ter Out 16, 2012 22:12
- 2 Respostas
- 2818 Exibições
- Última mensagem por e8group

Qui Out 18, 2012 11:11
Matrizes e Determinantes
-
- [Matrizes] Dúvida .
por e8group » Seg Out 22, 2012 23:06
- 2 Respostas
- 1506 Exibições
- Última mensagem por e8group

Ter Out 23, 2012 09:08
Matrizes e Determinantes
-
- duvida 3 questoes de matrizes
por naopercebo » Seg Out 24, 2011 22:03
- 1 Respostas
- 1138 Exibições
- Última mensagem por LuizAquino

Ter Out 25, 2011 10:29
Matrizes e Determinantes
-
- [Matrizes] Dúvida conceitual
por souzalucasr » Qua Ago 22, 2012 14:26
- 4 Respostas
- 4835 Exibições
- Última mensagem por souzalucasr

Qua Ago 29, 2012 12:34
Matrizes e Determinantes
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5156 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 A)^t =
A)^t =  A^t, onde
A^t, onde  ? K
? K 
 A)^t =
A)^t =  A^t, onde
A^t, onde  ? K
? K 
![[A]_{ij} = a_{ij} [A]_{ij} = a_{ij}](/latexrender/pictures/696f564a2df9d77962db1d56d1f617c8.png) para designar o termo geral da matriz e lembrando da definição de transposição de matrizes :
para designar o termo geral da matriz e lembrando da definição de transposição de matrizes : ![[A^t]_{ij} = [A]_{ji} = a_{ji} [A^t]_{ij} = [A]_{ji} = a_{ji}](/latexrender/pictures/bb4429fd8d2c473fce86883ea5eeeef3.png) (**) , temos que
(**) , temos que ![[(A^t)^t]_{ij} = [A^t]_{ji} = [A]_{ij} = a_{ij} [(A^t)^t]_{ij} = [A^t]_{ji} = [A]_{ij} = a_{ij}](/latexrender/pictures/a968c7178a1e4963ea162d4561724979.png) para todo
para todo 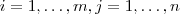 o que mostra
o que mostra  . No item b , utilize a definição (**) + propriedades dos números reais ,se não conseguir post . No item c , basta intercambiar a definição (**) juntamente com a definição produto de matrizes . Veja minha sugestão ,
. No item b , utilize a definição (**) + propriedades dos números reais ,se não conseguir post . No item c , basta intercambiar a definição (**) juntamente com a definição produto de matrizes . Veja minha sugestão , ![[(AB)^t]_{ij} = [AB]_{ji} = \sum_{k=1}^n a_{jk} \cdot b_{ki} [(AB)^t]_{ij} = [AB]_{ji} = \sum_{k=1}^n a_{jk} \cdot b_{ki}](/latexrender/pictures/164a9a91760a9c2213b4421a97d2384f.png) . Sendo o produto
. Sendo o produto 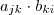 comutativo (pois ,
comutativo (pois , são números reais) e utilizando resultado do item (a) ,
são números reais) e utilizando resultado do item (a) , ![a_{jk} = [A^t]_{kj} , b_{kj} = [B^t]_{jk} a_{jk} = [A^t]_{kj} , b_{kj} = [B^t]_{jk}](/latexrender/pictures/bcc05bba66e675b80521c5cf67d26370.png) . Seguindo estas dicas conseguirá concluir o exercício .
. Seguindo estas dicas conseguirá concluir o exercício .
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.