 por Priscilla Correa » Seg Set 30, 2013 20:42
por Priscilla Correa » Seg Set 30, 2013 20:42
Olá, gostaria de ajuda nesse exercício:
Verifique se o subconjunto B do espaço vetorial V é uma base de V.
B = {1, 1+t, 1-t², 1-t-t²-t³}, V= P3(R).
Obrigada
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por Russman » Seg Set 30, 2013 20:56
por Russman » Seg Set 30, 2013 20:56
Para o subconjunto ser base é necessário q o mesmo seja LI. Verifique este fato.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Priscilla Correa » Seg Set 30, 2013 21:04
por Priscilla Correa » Seg Set 30, 2013 21:04
Eu sei que ele tem que ser LI, mas para mostrar isso eu multiplico eles por alfa, beta, gama e delta e igualo a "0"??
Obrigada
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por Russman » Seg Set 30, 2013 21:23
por Russman » Seg Set 30, 2013 21:23
Não necessariamente. Para B não ser LI basta que um dos vetores seja combinação linear dos demais( ou até mesmo só de um).
Exemplo:
O conjunto
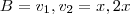
não é LI, pois
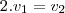
. Isto é,
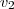
é escrito como combinação linear dos demais vetores do subconjunto.
No seu exemplo veja claramente que não existem coeficientes que multiplicados aos vetores resultam em um que esteja no conjunto. Assim, ele é LI e pode ser base do
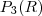
pois existem
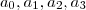
Reais tais que
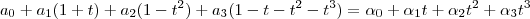
onde

é Real.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Priscilla Correa » Ter Out 01, 2013 00:28
por Priscilla Correa » Ter Out 01, 2013 00:28
Entendi, estou tento um pouco de dificuldade de entender algebra linear, poderia me dar umas dicas de como estudar??
Obrigada
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por Russman » Qua Out 02, 2013 00:15
por Russman » Qua Out 02, 2013 00:15
Faça exercícios. Faça montes deles até parecerem muito fáceis de resolver.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Priscilla Correa » Qua Out 02, 2013 05:04
por Priscilla Correa » Qua Out 02, 2013 05:04
Obrigada

-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por Cleyson007 » Qua Out 02, 2013 10:28
por Cleyson007 » Qua Out 02, 2013 10:28
Bom dia Priscilla!
Te enviei uma mensagem privada, espero que lhe ajude. Confere lá

Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Lógica Digital] Sistema Numérico Conversão Base X - Base 10
por Luc4sPaulo » Sex Fev 17, 2017 12:32
- 0 Respostas
- 4159 Exibições
- Última mensagem por Luc4sPaulo

Sex Fev 17, 2017 12:32
Lógica
-
- [Base] Encontrar uma base e a dimensão do subespaço
por anderson_wallace » Sex Jan 10, 2014 00:48
- 3 Respostas
- 13853 Exibições
- Última mensagem por Guilherme Pimentel

Qua Jan 15, 2014 05:23
Álgebra Linear
-
- [Mudança de Base] Matriz de mudança de base ? para ?.
por fabriel » Ter Nov 26, 2013 15:38
- 0 Respostas
- 2100 Exibições
- Última mensagem por fabriel

Ter Nov 26, 2013 15:38
Álgebra Linear
-
- Base !
por andy » Sex Nov 16, 2012 09:43
- 12 Respostas
- 8395 Exibições
- Última mensagem por e8group

Sex Nov 16, 2012 19:35
Cálculo: Limites, Derivadas e Integrais
-
- BASE
por Serdit » Sáb Fev 22, 2014 22:09
- 1 Respostas
- 1833 Exibições
- Última mensagem por marinalcd

Dom Fev 23, 2014 20:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




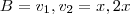 não é LI, pois
não é LI, pois 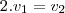 . Isto é,
. Isto é, 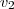 é escrito como combinação linear dos demais vetores do subconjunto.
é escrito como combinação linear dos demais vetores do subconjunto.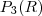 pois existem
pois existem 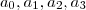 Reais tais que
Reais tais que 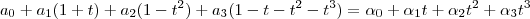
 é Real.
é Real.






 .
.



