 por crsjcarlos » Seg Jun 10, 2013 14:42
por crsjcarlos » Seg Jun 10, 2013 14:42
Determine
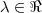
para que o seguinte subespaço de
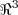
tenha dimensão 1.
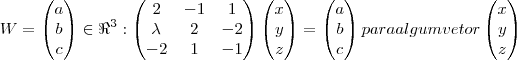
-
crsjcarlos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Dez 05, 2012 17:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MateusL » Qui Jul 18, 2013 00:14
por MateusL » Qui Jul 18, 2013 00:14
Como o subespaço tem dimensão 1, então
são três vetores colineares.
Então

e

são múltiplos de

.
Vamos dizer que:


Então:

Multiplicando a primeira linha por

e subtraindo a primeira da segunda obteremos:
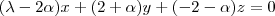
Como podemos ter qualquer valor para
e

, para que a equação acima seja verdadeira devemos ter:

De onde encontramos
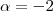
e, finalmente,

.
Apesar de não vir ao caso, é fácil ver que

.
Abraço!
EDITADO: Vi a resolução abaixo e me dei conta que havia errado ao escrever o valor de

. Agora o valor está certo!
Editado pela última vez por
MateusL em Qui Jul 18, 2013 22:59, em um total de 1 vez.
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Jul 18, 2013 21:21
por e8group » Qui Jul 18, 2013 21:21
Outra forma que pensei ...
Chamando de

a matriz que está multiplicando a matriz coluna

. Observando que a última linha da matriz

é múltipla da primeira ,segue
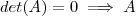
é singular

é um sistema compatível e indeterminado .Em particular , se

, então o sistema linear homogêneo

admite outras soluções além da trivial (1) . Agora , seja

.Então ,
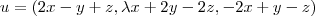
. Por outro lado ,

.
Definindo
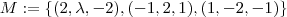
, por (1)
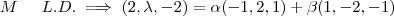
,daí resulta

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- GEOMETRIA ANALÍTICA - AJUDA, POR FAVOR!
por taisa_salles » Sex Mar 21, 2014 08:56
- 1 Respostas
- 1224 Exibições
- Última mensagem por taisa_salles

Sex Mar 21, 2014 08:59
Geometria Analítica
-
- [GEOMETRIA ANALÍTICA]AJUDEM POR FAVOR!
por Miya » Seg Abr 13, 2015 15:58
- 1 Respostas
- 1637 Exibições
- Última mensagem por adauto martins

Ter Abr 14, 2015 15:58
Geometria Analítica
-
- Geometria - ajuda por favor
por Janffs » Sex Dez 28, 2012 15:07
- 1 Respostas
- 1356 Exibições
- Última mensagem por young_jedi

Sex Dez 28, 2012 17:32
Geometria Plana
-
- Ajuda! Geometria analítica(Retas paralelas)
por nitwcst » Ter Mar 20, 2012 19:51
- 1 Respostas
- 1289 Exibições
- Última mensagem por MarceloFantini

Ter Mar 20, 2012 20:47
Geometria Analítica
-
- Questão de Geometria Analítica - Reta, ajuda!
por arthurvct » Seg Mai 27, 2013 15:28
- 1 Respostas
- 1436 Exibições
- Última mensagem por e8group

Ter Mai 28, 2013 21:34
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
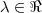 para que o seguinte subespaço de
para que o seguinte subespaço de  tenha dimensão 1.
tenha dimensão 1.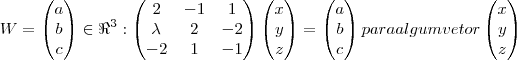

 para que o seguinte subespaço de
para que o seguinte subespaço de  tenha dimensão 1.
tenha dimensão 1.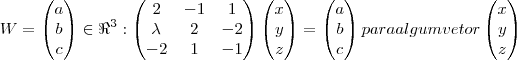

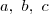 são três vetores colineares.
são três vetores colineares. e
e  são múltiplos de
são múltiplos de  .
.


 e subtraindo a primeira da segunda obteremos:
e subtraindo a primeira da segunda obteremos: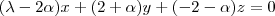
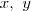 e
e  , para que a equação acima seja verdadeira devemos ter:
, para que a equação acima seja verdadeira devemos ter:
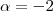 e, finalmente,
e, finalmente,  .
. .
. . Agora o valor está certo!
. Agora o valor está certo!
 a matriz que está multiplicando a matriz coluna
a matriz que está multiplicando a matriz coluna  . Observando que a última linha da matriz
. Observando que a última linha da matriz  é múltipla da primeira ,segue
é múltipla da primeira ,segue 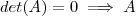 é singular
é singular  é um sistema compatível e indeterminado .Em particular , se
é um sistema compatível e indeterminado .Em particular , se  , então o sistema linear homogêneo
, então o sistema linear homogêneo  admite outras soluções além da trivial (1) . Agora , seja
admite outras soluções além da trivial (1) . Agora , seja  .Então ,
.Então , 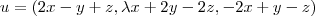 . Por outro lado ,
. Por outro lado ,  .
.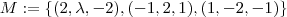 , por (1)
, por (1) 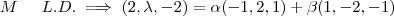 ,daí resulta
,daí resulta  .
.