Eis a questão:
Determine o ponto de interseção dos pares abaixo, caso exista, caso contrário, justifique:
a)dos planos
 e
e  ;
;Observando os dois planos, dá pra ver que preciso de um parâmetro pra equação do segundo. E só sei que é um plano porque o problema diz, como não confundir com uma reta, caso o problema não diga nada?
Prosseguindo... Eu dei um parâmetro pra segunda equação, da seguinte forma:
Colocando z = t, e substituindo de volta na equação anterior, obtive x = 1+ t e logo substitui essas informações na primeira equação(a do plano que foi dada) obtive:
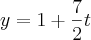
Tá... E agora? Devo descobrir o valor de t pra depois descobrir o valor das variáveis x, y e z?
A resposta do problema é a seguinte: a interseção destes 2 planos é a reta {(1 , 1, 0) + t(1, 7/2, 1}| t pertence a R}.
Notei que há uma parcialidade do valor em y nessa reta... Mas o que faço para obter os outros valores que estão descritos nessa reta? Foi isso que não entendi, além das outras dúvidas citadas acima... Por favor, me ajudem. Obrigado desde já!


 ), então a equação x - z = 1 representa uma reta no plano xOz (aqui O representa a origem do sistema).
), então a equação x - z = 1 representa uma reta no plano xOz (aqui O representa a origem do sistema). ), então a equação x - z = 1 representa um plano.
), então a equação x - z = 1 representa um plano.
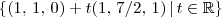 .
.
 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.