 por juniocs » Qua Set 19, 2012 09:44
por juniocs » Qua Set 19, 2012 09:44
Não consigo resolver essa matriz.
Determine A tal que: [ 2 2] + [1 2] A= [1 7]
[5 5 ] [3 5] [2 7]
-
juniocs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Set 19, 2012 09:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engª de Produção
- Andamento: cursando
 por Cleyson007 » Qua Set 19, 2012 09:51
por Cleyson007 » Qua Set 19, 2012 09:51
Bom dia Junio!
Seja bem-vindo ao AjudaMatemática!
Por favor, faça uso do LaTeX para postar suas dúvidas..
Seria isso????

Aguardo retorno

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por juniocs » Qua Set 19, 2012 10:48
por juniocs » Qua Set 19, 2012 10:48
Determine A tal que:

-
juniocs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Set 19, 2012 09:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engª de Produção
- Andamento: cursando
 por Cleyson007 » Qua Set 19, 2012 12:03
por Cleyson007 » Qua Set 19, 2012 12:03
Bom dia Junio!
Faça

Depois resolva a multiplicação:

O resultado que encontrar deverá ser somado com a matriz

e iguado com a matriz

Quanto a igualdade de matrizes deve ser observado elemento a elemento, ok?
Qualquer dúvida estou por aqui

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por juniocs » Qua Set 19, 2012 13:01
por juniocs » Qua Set 19, 2012 13:01
Eu Fiz assim:

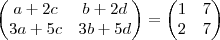
a+2c = 1 x(-3)
3a+5c = 2
-3a-6c = -3
3a+5c = 2
___________
-c = -1 x(-1)
c = 1
a+2.(1) = 1
a= 1-2
a= -1
b+2d = 7 x(-3)
3b+5d = 7
-3b-6d = -21
3b+5d = 7
___________
-d = -14 x(-1)
d = 14
b+2.(14) = 7
b= 7-28
b= -21
ficando assim:
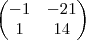
E agora como faço? dessa forma ? se somar as duas não bate com valor depois da igualdade.
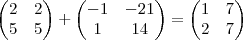
-
juniocs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Set 19, 2012 09:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engª de Produção
- Andamento: cursando
 por vmo_apora » Qua Set 19, 2012 13:22
por vmo_apora » Qua Set 19, 2012 13:22
Na verdade você encontrou a matriz

. Faça

e depois some com

-
vmo_apora
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Mai 13, 2011 16:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por juniocs » Qua Set 19, 2012 14:19
por juniocs » Qua Set 19, 2012 14:19
-
juniocs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Set 19, 2012 09:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engª de Produção
- Andamento: cursando
 por Cleyson007 » Qua Set 19, 2012 15:16
por Cleyson007 » Qua Set 19, 2012 15:16
Boa tarde Junio!
Acompanhe!

Resolvendo, temos:

Tente a partir daqui.. (Eu já fiz e realmente o valor "bate").
Comente qualquer dúvida

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por juniocs » Qua Set 19, 2012 15:40
por juniocs » Qua Set 19, 2012 15:40
Boa tarde, Cleyson.
Eu já tentei fazer e não consigo, tenho que entregar um trabalho hoje e falta esta questão. Da forma que você fez, eu vou somar a primeira matriz com segunda que tem as variáveis? qual que tem que ser o resultado desta questão? Esta questão ela não foi explicada em classe, por isso não estou conseguindo fazer. Peço sua ajuda. Obrigado.
-
juniocs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Set 19, 2012 09:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engª de Produção
- Andamento: cursando
 por Cleyson007 » Qua Set 19, 2012 16:05
por Cleyson007 » Qua Set 19, 2012 16:05
Boa tarde Junior!
Vamos lá!
Sim, soma-se das duas matrizes, veja:
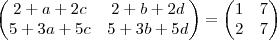
Chegamos aos sistemas de equações:
2 + a + 2c = 1
5 + 3a + 5c = 2 "
Resolvendo, encontra-se a = -1 e c = 0"
2 + b + 2d = 7
5 + 3b + 5d = 7 "
Resolvendo, encontra-se d = 13 e b = -21"
Logo,


Resolvendo,

. Logo, provamos a igualdade das matrizes!
Ok?

Atenciosamente,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por juniocs » Qua Set 19, 2012 16:51
por juniocs » Qua Set 19, 2012 16:51
Boa Tarde, Cleyson.
É isso aí mesmo, agora consegui entender como se resolve esta questão, muito obrigado pela sua atenção, me ajudou muito, realmente eu não conseguiria resolvê-la sozinho, pois não tivemos a devida orientação em classe. Valeu, muito obrigado.
Att.
-
juniocs
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Set 19, 2012 09:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engª de Produção
- Andamento: cursando
 por Cleyson007 » Qua Set 19, 2012 17:10
por Cleyson007 » Qua Set 19, 2012 17:10
Boa tarde Junio!
Fico feliz em saber que te ajudei..
Sempre que precisar conte com a minha ajuda e com a dos demais usuários do fórum.
Desejo-lhe um bom trabalho e sucesso em seus estudos

Atenciosamente,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como resolver equação diofantina utilizndo matrizes?
por joaofonseca » Qui Dez 13, 2012 17:25
- 2 Respostas
- 2957 Exibições
- Última mensagem por joaofonseca

Sex Dez 14, 2012 11:51
Teoria dos Números
-
- Como resolver matrizes
por zaza_mansano » Qua Out 19, 2011 12:36
- 2 Respostas
- 5190 Exibições
- Última mensagem por zaza_mansano

Qui Out 20, 2011 22:04
Matrizes e Determinantes
-
- matrizes COMO RESOLVER???
por LEANDRO HENRIQUE » Dom Mar 09, 2014 16:22
- 0 Respostas
- 1736 Exibições
- Última mensagem por LEANDRO HENRIQUE

Dom Mar 09, 2014 16:22
Matrizes e Determinantes
-
- como resolver essa multiplicaçao de matrizes
 por weverton » Sáb Jul 24, 2010 06:14
por weverton » Sáb Jul 24, 2010 06:14
- 2 Respostas
- 3464 Exibições
- Última mensagem por weverton

Dom Jul 25, 2010 23:02
Matrizes e Determinantes
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8708 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.










 e iguado com a matriz
e iguado com a matriz 



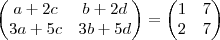
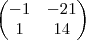
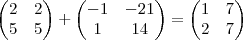

 . Faça
. Faça  e depois some com
e depois some com

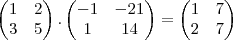
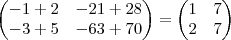








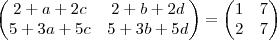


 . Logo, provamos a igualdade das matrizes!
. Logo, provamos a igualdade das matrizes!




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.