Vou tentar explicar de maneira rápida.
Dados dois espaços vetoriais e uma transformação linear, você pode definir o
núcleo ou
kernel da transformação linear como todos os vetores tais que a transformação se anula, ou seja, dada

o núcleo é o conjunto dos vetores que anulam a transformação:

.
Os vetores que não anulam a transformação vão para o conjunto
imagem. Existe um teorema que diz que
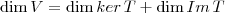
.
Chamamos de
nulidade a dimensão do núcleo da transformação, ou seja,

. Nulidade positiva significa que a dimensão é maior que zero. Convencionamos que quando o único vetor no núcleo é o vetor nulo então sua dimensão é zero.
Existe um outro teorema que diz que uma transformação é invertível
se e somente se a nulidade for zero, ou seja, o único vetor no núcleo é o vetor nulo.
De maneira sintética, dado um subespaço, dizemos que o seu complemento ortogonal é composto por todos os vetores que são ortogonais entre si, ou seja, usando o produto interno do espaço nós temos que

, onde W é um subespaço de V e
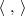
é o produto interno do espaço.
Usando este pedaço de teoria, veja se consegue resolver. Procure um pouco mais sobre complementos ortogonais, estou sem tempo pra poder explicar tudo.




 o núcleo é o conjunto dos vetores que anulam a transformação:
o núcleo é o conjunto dos vetores que anulam a transformação:  .
. 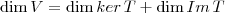 .
. . Nulidade positiva significa que a dimensão é maior que zero. Convencionamos que quando o único vetor no núcleo é o vetor nulo então sua dimensão é zero.
. Nulidade positiva significa que a dimensão é maior que zero. Convencionamos que quando o único vetor no núcleo é o vetor nulo então sua dimensão é zero. , onde W é um subespaço de V e
, onde W é um subespaço de V e 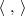 é o produto interno do espaço.
é o produto interno do espaço.

 , avisa que eu resolvo.
, avisa que eu resolvo.

