 por tigerwong » Sáb Jun 30, 2012 01:16
por tigerwong » Sáb Jun 30, 2012 01:16
Como Resolver?
24) Dois capitais foram aplicados na mesma data numa instituição financeira com prazo de dois anos. Sabendo-se que a diferença entre o maior e o menor montava a R$10.000,00 na data da aplicação e que aumentou para R$12.100,00 no vencimento, a taxa anula de juros compostos corresponde a:
A 8,5%
B 9%
C 9,5%
D 10,0%
E 11,0%
-
tigerwong
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jun 24, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por DanielFerreira » Ter Ago 28, 2012 19:41
por DanielFerreira » Ter Ago 28, 2012 19:41
tigerwong escreveu:Como Resolver?
24) Dois capitais foram aplicados na mesma data numa instituição financeira com prazo de dois anos. Sabendo-se que a diferença entre o maior e o menor montava a R$10.000,00 na data da aplicação e que aumentou para R$12.100,00 no vencimento, a taxa anula de juros compostos corresponde a:
A 8,5%
B 9%
C 9,5%
D 10,0%
E 11,0%
CAPITAL I:
Capital (P): x
Prazo (n): 2 anos
Taxa (i) = ?
Montante: S_1
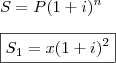 CAPITAL II
CAPITAL II:
Capital (P): y
Prazo (n): 2 anos
Taxa (i) = ?
Montante: S_2
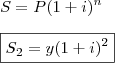
tigerwong escreveu:... Sabendo-se que a diferença entre o maior e o menor montava a R$10.000,00 na data da aplicação...
tigerwong escreveu:... e que aumentou para R$12.100,00 no vencimento, ...
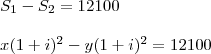
Do sistema:
![\\ \begin{cases} x - y = 10000 \\ x(1 + i)^2 - y(1 + i)^2 = 12100\end{cases} \\\\\\ \begin{cases} x - y = 10000 \\ (1 + i)^2[x - y] = 12100\end{cases} \\ \begin{cases} x - y = 10000 \\ x(1 + i)^2 - y(1 + i)^2 = 12100\end{cases} \\\\\\ \begin{cases} x - y = 10000 \\ (1 + i)^2[x - y] = 12100\end{cases}](/latexrender/pictures/6dc482dad4423c28ee5d1d8363073524.png)
Temos:
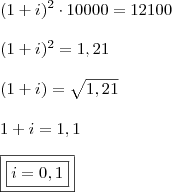
Ou seja,
i = 10% Espero ter ajudado!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- uma questão de juros compostos?
por aprendiz da vida » Qua Mai 05, 2010 14:02
- 2 Respostas
- 1793 Exibições
- Última mensagem por aprendiz da vida

Qua Mai 05, 2010 16:32
Matemática Financeira
-
- QUESTÃO DE JUROS COMPOSTOS
por braga104 » Seg Mai 06, 2013 19:25
- 0 Respostas
- 1117 Exibições
- Última mensagem por braga104

Seg Mai 06, 2013 19:25
Matemática Financeira
-
- Questão Urgente de juros simples e compostos
 por Raisson jose » Seg Fev 29, 2016 22:15
por Raisson jose » Seg Fev 29, 2016 22:15
- 1 Respostas
- 3891 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 05, 2016 09:54
Matemática Financeira
-
- Ajuda para resolver questão de juros compostos
por reuel » Qua Jan 09, 2013 17:34
- 1 Respostas
- 2682 Exibições
- Última mensagem por Cleyson007

Sex Jan 11, 2013 17:09
Matemática Financeira
-
- Ajuda para resolver 4 questão de juros compostos por favor
por reuel » Qua Mar 20, 2013 00:58
- 1 Respostas
- 5953 Exibições
- Última mensagem por leticiaac

Seg Mar 02, 2015 17:20
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


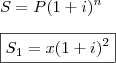
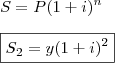
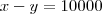
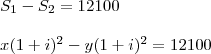
![\\ \begin{cases} x - y = 10000 \\ x(1 + i)^2 - y(1 + i)^2 = 12100\end{cases} \\\\\\ \begin{cases} x - y = 10000 \\ (1 + i)^2[x - y] = 12100\end{cases} \\ \begin{cases} x - y = 10000 \\ x(1 + i)^2 - y(1 + i)^2 = 12100\end{cases} \\\\\\ \begin{cases} x - y = 10000 \\ (1 + i)^2[x - y] = 12100\end{cases}](/latexrender/pictures/6dc482dad4423c28ee5d1d8363073524.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.