 por brunotst » Dom Ago 15, 2010 12:09
por brunotst » Dom Ago 15, 2010 12:09
Pessoal não estou conseguindo resolver este seguinte problema, por favor me ajudem.
Uma fatura de no valor de R$8.763,00 sofreu um desconto de 6,3% e, em seguida, um outro desconto(sobre o valor da fatura menos o primeiro desconto) que fez com que seu valor líquido passasse a ser de R$8.000,00. Determine o percentual do segundo desconto.
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por alexandre32100 » Dom Ago 15, 2010 21:51
por alexandre32100 » Dom Ago 15, 2010 21:51
-
alexandre32100
-
 por alexandre32100 » Dom Ago 15, 2010 21:59
por alexandre32100 » Dom Ago 15, 2010 21:59
-
alexandre32100
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Descontos
por karlinhaa » Qui Dez 02, 2010 15:19
- 2 Respostas
- 1246 Exibições
- Última mensagem por karlinhaa

Qui Dez 02, 2010 16:05
Matemática Financeira
-
- Descontos
por karlinhaa » Qui Dez 09, 2010 13:47
- 4 Respostas
- 2007 Exibições
- Última mensagem por my2009

Sex Dez 10, 2010 13:31
Matemática Financeira
-
- Descontos e Lucros
por karinaforlin » Sáb Abr 03, 2010 22:58
- 0 Respostas
- 2605 Exibições
- Última mensagem por karinaforlin

Sáb Abr 03, 2010 22:58
Matemática Financeira
-
- descontos urgente
por karlinhaa » Qui Dez 09, 2010 14:14
- 0 Respostas
- 666 Exibições
- Última mensagem por karlinhaa

Qui Dez 09, 2010 14:14
Matemática Financeira
-
- 1 Descontos Simples e 1 JUROS COMPOSTOS
por william1993 » Sáb Jan 26, 2013 03:13
- 0 Respostas
- 2391 Exibições
- Última mensagem por william1993

Sáb Jan 26, 2013 03:13
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 (porcentagem equivalente ao novo valor:
(porcentagem equivalente ao novo valor:  )
)


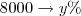

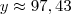
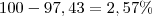


 .
.
 :
: