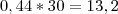Dados:
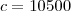
R$

R$
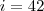
% a.a
Data inicial: 20/01/2000
Já que trata-se do
juros composto, temos que calcular primeiro o montante, a partir do capital inicial e do
juros final, logo:
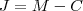


R$
Agora, utilizamos o valor na fórmula do montante para descobrir a quantidade de anos:

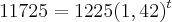

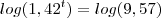
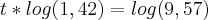
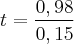
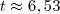
anos
Logo, mudamos a data, a princípio para 20/01/2006, já que 6 é o número inteiro do período de tempo. Depois, fazemos

para encontrar o valor restante em dias.
Considerando que todos os meses têm 30 dias, isso nos para o dia 20/07/2006, pois

.
Logo, resta multiplicar os 0,44 restantes para descobrir a quantidade de dias:
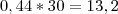
Assim, ignoramos o 0,2, por corresponder a horas e, acrescentamos 13 dias, portanto, a data final é 13/08/2006.
Espero ter pelo menos ajudado a dar uma noção de como resolver problemas de
juros compostos.



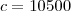 R$
R$ R$
R$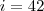 % a.a
% a.a 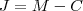

 R$
R$
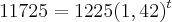

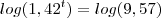
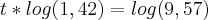
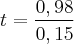
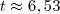 anos
anos para encontrar o valor restante em dias.
para encontrar o valor restante em dias. .
.