Carol,
bom dia!
Deverás converter a taxa, de semestre para bimestre, e, fazer o mesmo com o prazo!
Ao se tratar de Juros Compostos, sempre converta a taxa de acordo com o prazo, neste caso (seu exercício), a capitalização é bimestral, portanto,...
Para converter a taxa, aplicamos o 'método' conhecido como Taxa Equivalente.
Alguns exemplos:
- supomos que o prazo esteja em meses e a taxa seja anual, então fazemos:

;
- supomos que o prazo esteja em dias e a taxa seja anual, então fazemos:
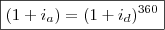
;
- supomos que o prazo esteja em dias e a taxa seja mensal, então fazemos:

;
- (...);
- supomos que o prazo seja bimestral e a taxa semestral, então fazemos:

.
Segue,
![\\ (1 + i_s) = (1 + i_b)^3 \\\\ (1 + 0,24) = (1 + i_b)^3 \\\\ (1 + i_b)^3 = 1,24 \\\\ 1 + i_b = \sqrt[3]{1,24} \\\\ 1 + i_b = 1,0743 \\\\ \boxed{\boxed{i_b = 0,0743}} \\ (1 + i_s) = (1 + i_b)^3 \\\\ (1 + 0,24) = (1 + i_b)^3 \\\\ (1 + i_b)^3 = 1,24 \\\\ 1 + i_b = \sqrt[3]{1,24} \\\\ 1 + i_b = 1,0743 \\\\ \boxed{\boxed{i_b = 0,0743}}](/latexrender/pictures/63a90ea4392496963f737db7f2fcfeb7.png)
Isto é,
7,43% a.b Consegues prosseguir? Caso contrário, retorne informando tua a dúvida, ok?!
Tens o gabarito?
Até!
Daniel.


 ;
;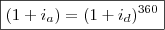 ;
; ;
; .
.![\\ (1 + i_s) = (1 + i_b)^3 \\\\ (1 + 0,24) = (1 + i_b)^3 \\\\ (1 + i_b)^3 = 1,24 \\\\ 1 + i_b = \sqrt[3]{1,24} \\\\ 1 + i_b = 1,0743 \\\\ \boxed{\boxed{i_b = 0,0743}} \\ (1 + i_s) = (1 + i_b)^3 \\\\ (1 + 0,24) = (1 + i_b)^3 \\\\ (1 + i_b)^3 = 1,24 \\\\ 1 + i_b = \sqrt[3]{1,24} \\\\ 1 + i_b = 1,0743 \\\\ \boxed{\boxed{i_b = 0,0743}}](/latexrender/pictures/63a90ea4392496963f737db7f2fcfeb7.png)





 .
.
 :
: