pois bem... tenho alguns problemas que não estou conseguindo resolver... como são todos do mesmo estilo, vou colocar somente um e acho que já será o suficiente.
1. Encontre a taxa de juros necessária para fazer um investimento de 5000 reais chegar a 7500 (reais) em três anos, com juro composto mensalmente.
as fórmulas que tenho disponíveis são: juros simples
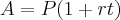; juros compostos 
; sendo que:A= montante acumulado
P= principal ou capital inicial
r= taxa de juros nominal anual
m= número de períodos de conversão ao ano
t= prazo (número de anos)
a resposta para o problema é 13,59% ao ano
obs.: vou mostrar o que tentei fazer, não sei se é o caminho certo:
Acho que há uma forma melhor de resolver isso, mas não vejo como... se alguém puder me dar uma ajudinha...
vlw?
![\Rightarrow \sqrt[36]{1,5}=\sqrt[36]{{(1+\frac{x}{12})}^{36}} \Rightarrow 1,011326585 = \left(1+\frac{x}{12} \right) \Rightarrow ...](/latexrender/pictures/af845b4213f368809bf1f22d1a774853.png "\Rightarrow \sqrt[36]{1,5}=\sqrt[36]{{(1+\frac{x}{12})}^{36}} \Rightarrow 1,011326585 = \left(1+\frac{x}{12} \right) \Rightarrow ...")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.