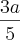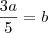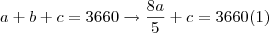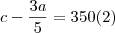por DMonteiro » Sáb Abr 03, 2010 23:31
por DMonteiro » Sáb Abr 03, 2010 23:31
Certo dia um correntista fez três depósitos, de valores A, B e C reais, num total de R$ 3660,00. Se de C subtrairmos B, obtemos R$ 350,00 e B corresponde a 3/5 de A. O menor desses três depósitos foi de:
a) R$ 879,00
b) R$ 915,00
c) R$ 1021,35
d) R$ 1220,00
e) R$ 1326,35
-
DMonteiro
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 03, 2010 22:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por estudandoMat » Dom Abr 04, 2010 12:46
por estudandoMat » Dom Abr 04, 2010 12:46
Tá certo esses valores?
pq eu fiz assim:
a+b+c = 3660
c - b = 350
b =
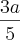
mas não chego de jeito nenhum em nenhuma das opções. O minimo q axei foi b = 902,72
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DMonteiro » Dom Abr 04, 2010 15:01
por DMonteiro » Dom Abr 04, 2010 15:01
Esta certo porque eu tirei essa questão de uma prova que foi dada no Concurso da Caixa Federal de 2004.
E não consegui resolvê-la de forma alguma.
As 5 opções de respostas, era as que continha na Prova.
Mesmo assim obrigado por me ajudar a resolver esse problema, abraço.
-
DMonteiro
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 03, 2010 22:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Marcampucio » Dom Abr 04, 2010 15:12
por Marcampucio » Dom Abr 04, 2010 15:12
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por gambit » Ter Fev 17, 2015 00:00
por gambit » Ter Fev 17, 2015 00:00
simples
C-B= 305 OBVIO Q C>B
B= 3/5 DE A OBVIO Q B<A então B é o menor deposito.
daí é só trabalhar com as respostas
B=915+305 obtemos o valor de C=1220.
B=3/5 de A = 915/3=305 x 5 obtemos o valor de A=1525
então o menor deposito é o de B= 915.
-
gambit
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Fev 16, 2015 23:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: técnico em tst
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguém sabe como resolver???
por DMonteiro » Sáb Abr 03, 2010 23:38
- 4 Respostas
- 3115 Exibições
- Última mensagem por DMonteiro

Dom Abr 04, 2010 21:40
Cálculo: Limites, Derivadas e Integrais
-
- [Equaçoes] alguem que sabe me ajude a resolver.
por teilom » Dom Ago 04, 2013 17:00
- 1 Respostas
- 1482 Exibições
- Última mensagem por DanielFerreira

Dom Ago 04, 2013 20:03
Equações
-
- [Limite] alguem sabe resolver essa expressão?
por tainaraabp » Ter Out 02, 2012 11:35
- 1 Respostas
- 2058 Exibições
- Última mensagem por LuizAquino

Ter Out 02, 2012 12:25
Cálculo: Limites, Derivadas e Integrais
-
- Por favor alguém sabe resolver esta questão
por costav13 » Sáb Nov 09, 2013 10:10
- 3 Respostas
- 2573 Exibições
- Última mensagem por e8group

Dom Nov 10, 2013 13:29
Cálculo: Limites, Derivadas e Integrais
-
- Integral Alguém sabe resolver esse problema
por JorgeHenr » Seg Out 03, 2016 16:32
- 1 Respostas
- 3993 Exibições
- Última mensagem por egouni

Seg Out 17, 2016 17:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.