 por Ronaldobb » Qui Fev 07, 2013 11:28
por Ronaldobb » Qui Fev 07, 2013 11:28
Se aplicarmos determinada quantia durante 8 meses, seu montante será de R$63.000,00. Caso a aplicação durasse 13 meses, o montante seria de R$74.250,00. Qual a taxa mensal empregada?
Minha resolução:
Eu usei o primeiro montante R$63.000,00 como o Capital "C" e o segundo Montante como o Montante da aplicação e diminui 13 - 8 = 5 meses e fiz a conta de juros simples normalmente, mas não achei a resposta nas alternativas! Poderiam me ajudar?
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por e8group » Qui Fev 07, 2013 14:27
por e8group » Qui Fev 07, 2013 14:27
Tem gabarito ? Pensei em fazer assim , considere
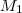
e

valores acumulado, soma do Capital Inicial com o juro

produzido em determinado tempo

e
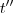
,i.e.,
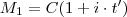
e

. Dividindo

por
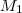
(os C's cancelam ) ,

.Esta igualdade permite calcular a taxa

em função de
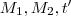
e
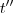
Observe que :

Calculei i = 0,05 ou i = 5% .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ronaldobb » Qui Fev 07, 2013 16:57
por Ronaldobb » Qui Fev 07, 2013 16:57
Poderia por gentileza resolvê-lo passo a passo pra mim, pois não entendi como você chegou ao resultado. Grato!
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por e8group » Qui Fev 07, 2013 18:05
por e8group » Qui Fev 07, 2013 18:05
Montante não é valor acumulado, soma do Capital Inicial com o juro produzido em determinado tempo ?
Isto é ,
Juros :

. (1)
Montante :

. (2)
Note que o capital

e a taxa de juros

são valores fixos ,então à medida que o tempo passa o juros (J) e o motante (M) varia .
Para facilitar as contas ,ao invés de susbstituirmos os valores fornecidos pelo enunciado na expressão (2) , vamos supor que passado

e
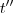
meses tenhamos montantes
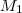
e

.
Hipótese :
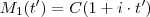
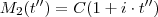
Disso teremos ,

e
ainda ,
![M_1(t')[1+i\cdot t''] = M_2(t'')[1+i\cdot t'] M_1(t')[1+i\cdot t''] = M_2(t'')[1+i\cdot t']](/latexrender/pictures/8966023a2dc2c2451e20771160741546.png)

Deixando o termo

em evidência ,
![M_1(t') -M_2(t'') + i[M_1(t') \cdot t'' - M_2(t'') \cdot t'] = 0 M_1(t') -M_2(t'') + i[M_1(t') \cdot t'' - M_2(t'') \cdot t'] = 0](/latexrender/pictures/71bb81286efe906f6ce80fa2644b1bb0.png)
E obtemos a seguinte fórmula ,que relaciona a taxa de juros

em função dos montantes
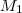
e

.
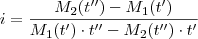
. (3)
Portanto basta relacionar os dados do enunciado com a fórmula obtida acima .
Deste modo :
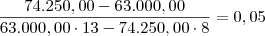
ou 5 % .
OBS.: A vantagem desta fórmula é que para quaisquer exercícios desta mesma linha ,mas com montantes diferentes , a solução para

decorre da expressão (3) .
Estar correto ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por DanielFerreira » Dom Fev 10, 2013 21:11
por DanielFerreira » Dom Fev 10, 2013 21:11
Outra forma de abordar o problema seria...
Aplicação I:
Prazo (n): 8 meses
Montante (S): R$ 63.000,00
Capital (P): P
Taxa (i): i
Sabe-se que

, então:
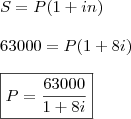 Aplicação II
Aplicação II:
Prazo (n): 13 meses
Montante (S): R$ 74.250,00
Capital (P): P
Taxa (i): i

Igualando P...

simplificando os numeradores por 250;

por 9;

Isto é,
5% a.m"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda juros simples
por crismara » Seg Dez 06, 2010 11:38
- 0 Respostas
- 1303 Exibições
- Última mensagem por crismara

Seg Dez 06, 2010 11:38
Matemática Financeira
-
- ajuda juros simples
por karlinhaa » Seg Dez 06, 2010 15:48
- 2 Respostas
- 1728 Exibições
- Última mensagem por karlinhaa

Ter Dez 07, 2010 10:34
Matemática Financeira
-
- Ajuda para resolver 4 questão de juros compostos por favor
por reuel » Qua Mar 20, 2013 00:58
- 1 Respostas
- 5959 Exibições
- Última mensagem por leticiaac

Seg Mar 02, 2015 17:20
Matemática Financeira
-
- Juros Simples // Juros Compostos
por Roberta » Qui Jul 16, 2009 18:22
- 3 Respostas
- 8206 Exibições
- Última mensagem por Roberta

Qui Jul 16, 2009 19:46
Matemática Financeira
-
- Juros Simples
por Gir » Ter Set 01, 2009 11:03
- 1 Respostas
- 8303 Exibições
- Última mensagem por Lucio Carvalho

Ter Set 01, 2009 17:24
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


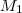 e
e  valores acumulado, soma do Capital Inicial com o juro
valores acumulado, soma do Capital Inicial com o juro  produzido em determinado tempo
produzido em determinado tempo  e
e 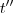 ,i.e.,
,i.e., 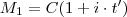 e
e  . Dividindo
. Dividindo  .Esta igualdade permite calcular a taxa
.Esta igualdade permite calcular a taxa 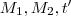 e
e 

 . (1)
. (1)  . (2)
. (2)  e a taxa de juros
e a taxa de juros 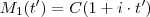
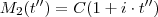

![M_1(t')[1+i\cdot t''] = M_2(t'')[1+i\cdot t'] M_1(t')[1+i\cdot t''] = M_2(t'')[1+i\cdot t']](/latexrender/pictures/8966023a2dc2c2451e20771160741546.png)

![M_1(t') -M_2(t'') + i[M_1(t') \cdot t'' - M_2(t'') \cdot t'] = 0 M_1(t') -M_2(t'') + i[M_1(t') \cdot t'' - M_2(t'') \cdot t'] = 0](/latexrender/pictures/71bb81286efe906f6ce80fa2644b1bb0.png)
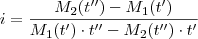 . (3)
. (3) 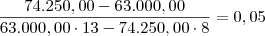 ou 5 % .
ou 5 % .  , então:
, então: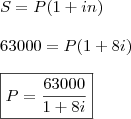







 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.