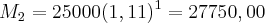Renata Francisco escreveu:Boa noite,
Estou com 5 exercícios um pouco complicados para fazer, alguém pode me ajudar pelo menos em 1:
1º) O Sr. Joaquim, possuidor de uma importância na ordem de R$50.000,00 empresta, quantias iguais, a dois tomadores, de forma que a diferença entre as taxas utilizadas nas operações foi de 2%. Se sua remuneração final foi de R$5.000,00. Que taxas são estas?
Obrigada desde já!
Forte abraço a todos.
Renata, eu faria assim:
Como o montante final é 55.000,00 e as aplicações iniciais são iguais, então são dois capitais de 25.000,00 afetados de duas taxas diferentes. Como o problema não fala em período, façamos o expoente da fórmula ser 1.
Embora sejam duas taxas, o enunciado dá a dica de que a segunda taxa é a mesma primeira, mais 2%. Então não escreveremos duas incógnitas para representar a taxa, mas uma só, a letra 'i':

(Soma-se 0,02 ao invés de 2% porque a idéia não é usar a taxa percentual para aplicação na fórmula, mas sim a unitária, que é, no caso 2%/100)
Ou seja, retirando os expoentes porque são desnecessários, e separando as incógnitas das constantes, temos
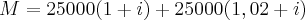
Acontece que M = 55.000, de modo que
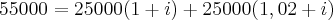
Explicitando 25000,00, ficamos
![55000 = {25000 [(1+i) + (1,02+i)]} 55000 = {25000 [(1+i) + (1,02+i)]}](/latexrender/pictures/0c2e707ebe631e5e67d08590e3a69b34.png)
Continuando a racionalização

Como nosso objetivo é explicitar o a taxa 'i', temos

, assim como

, assim como

Sendo i=0,09, dois por cento de diferença na segunda taxa, conforme enunciado, será j=0,11.
Então as taxas são 9% por 1 período completo e 11% pelo mesmo período.
Tirando a prova:

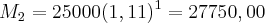

Espero ter ajudado.



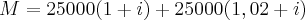
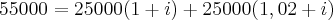
![55000 = {25000 [(1+i) + (1,02+i)]} 55000 = {25000 [(1+i) + (1,02+i)]}](/latexrender/pictures/0c2e707ebe631e5e67d08590e3a69b34.png)

 , assim como
, assim como  , assim como
, assim como