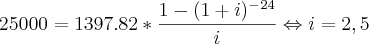
Primeiro passei o 1397.82 para o primeiro termo do sistema ficando a dividir por 25000. E é aí que surge o problema. Como faço para me livrar da potência -24? já tentei elevar tudo ao inverso (1/-24) mas sem solução porque o i de baixo não está elevado ao mesmo expoente.
E os meus conhecimentos param por aí. No meu caderno de matematica financeira têm lá umas propriedades dos logaritmos mas eu não sei interpretar direito. Seria possivel resolver isto através de logaritmos?
Obrigado pela vossa ajuda.
Cumprimentos,
Edgar Gomes




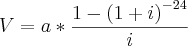

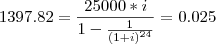

 .
.



