 por adrianosaldanha » Seg Mai 16, 2011 16:13
por adrianosaldanha » Seg Mai 16, 2011 16:13
Ana aplicou R$ 20.000,00 a juros compostos durante 2 meses e resgatou, ao final do prazo, R$ 21.632,00.A taxa anual da aplicação foi de
(A) 60,10%
(B) 58,18%*************
(C) 48,00%
(D) 42,58%
(E) 36,00%
Considere: Fator de acumulação 2- 1,0816 - (1+i)n
p.s. parei em 1,0816 e depois deu brancoooooooooooooooooooooooooooooo....
-
adrianosaldanha
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Jul 21, 2009 13:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: concursos
- Andamento: formado
 por my2009 » Ter Mai 17, 2011 13:08
por my2009 » Ter Mai 17, 2011 13:08
Olá tudo bem ? Geralmente eu consigo resolver problemas q envolvam taxa assim:
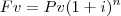
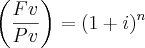
![\sqrt[n]{\left(\frac{Fv}{Pv} \right)}= \sqrt[n]{(1+i)^n} \sqrt[n]{\left(\frac{Fv}{Pv} \right)}= \sqrt[n]{(1+i)^n}](/latexrender/pictures/b3cbade151f7efa8906c1e17236926d3.png)
![i= n\sqrt[]{\left(\frac{Fv}{Pv} \right)}-1 i= n\sqrt[]{\left(\frac{Fv}{Pv} \right)}-1](/latexrender/pictures/707823a785794550744c2ce11e80d056.png)
Mesmo assim não deu certo.. Na verdade , eu nao entendi qual é o fator de acumulação.
Alguém pode NOS ajudar !!!!!!!!!!!
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cesgranrio – tec adm controle jr – parte conhec especif
por adrianosaldanha » Seg Mai 16, 2011 16:10
- 0 Respostas
- 1246 Exibições
- Última mensagem por adrianosaldanha

Seg Mai 16, 2011 16:10
Matemática Financeira
-
- Cesgranrio – tec adm controle jr – parte conhec especif
por adrianosaldanha » Seg Mai 16, 2011 16:12
- 0 Respostas
- 1046 Exibições
- Última mensagem por adrianosaldanha

Seg Mai 16, 2011 16:12
Matemática Financeira
-
- Cesgranrio – tec adm controle jr – parte conhec especif
por adrianosaldanha » Seg Mai 16, 2011 16:14
- 0 Respostas
- 989 Exibições
- Última mensagem por adrianosaldanha

Seg Mai 16, 2011 16:14
Matemática Financeira
-
- Cesgranrio – tec adm controle jr – parte conhec especif
por adrianosaldanha » Seg Mai 16, 2011 16:20
- 0 Respostas
- 923 Exibições
- Última mensagem por adrianosaldanha

Seg Mai 16, 2011 16:20
Matemática Financeira
-
- b-spline passando por vertice de controle
por srabates » Qua Fev 22, 2012 22:36
- 0 Respostas
- 2340 Exibições
- Última mensagem por srabates

Qua Fev 22, 2012 22:36
Dúvidas Pendentes (aguardando novos colaboradores)
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


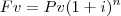
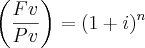
![\sqrt[n]{\left(\frac{Fv}{Pv} \right)}= \sqrt[n]{(1+i)^n} \sqrt[n]{\left(\frac{Fv}{Pv} \right)}= \sqrt[n]{(1+i)^n}](/latexrender/pictures/b3cbade151f7efa8906c1e17236926d3.png)
![i= n\sqrt[]{\left(\frac{Fv}{Pv} \right)}-1 i= n\sqrt[]{\left(\frac{Fv}{Pv} \right)}-1](/latexrender/pictures/707823a785794550744c2ce11e80d056.png)


 .
.



