Em geral, apenas enunciados de exercícios.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Madjer » Sex Set 10, 2010 09:48
por Madjer » Sex Set 10, 2010 09:48
Cinco rapazes e as respectivas namoradas foram jantar a um restaurante. De quantas maneiras diferentes se podem dispor os dez jovens numa mesa rectangular, com 5 lugares de cada lado, de tal modo que os 2 membros de cada par de namorados fiquem frente a frente! Numa pequena composicao explica o teu raciocinio.
Eu tentei desenhar a mesa e colocar os lugares dos rapazes e das raparigas e cheguei a um resultado e 5! x 5! mas n esta igual a resposta do professor. Podem me ajudar?
-
Madjer
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Set 10, 2010 09:38
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: formado
 por MarceloFantini » Sex Set 10, 2010 19:01
por MarceloFantini » Sex Set 10, 2010 19:01
Eu visualizei o problema assim: Suponha que temos a mesa com 10 lugares. Temos dez opções para esse lugar (qualquer rapaz ou menina pode sentar-se). Porém, ao sentar, automaticamente determina-se o assento oposto (pois o casal tem que ficar de frente). Então sobram 8 opções para o próximo, e o raciocínio é análogo. Então:
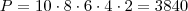
É essa a resposta?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Sex Set 10, 2010 21:56
por Elcioschin » Sex Set 10, 2010 21:56
Fantini
A sua visualização foi perfeita quanto à distribuição dos 5 casais
Entretanto acho que cada rapaz pode trocar de lugar com sua namorada.
O que você acha?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por MarceloFantini » Sex Set 10, 2010 22:14
por MarceloFantini » Sex Set 10, 2010 22:14
Já está incluído nessa conta. Veja uma outra maneira:
A distribuição dos rapazes nas 5 cadeiras é
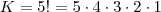
. Porém, cada rapaz pode trocar de lugar com a namorada, ou seja, cada lugar pode trocar 2 vezes:
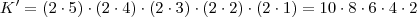
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Madjer » Seg Set 13, 2010 14:14
por Madjer » Seg Set 13, 2010 14:14
ja descobri a resposta...
e 5! e depois cada namorada pode trocar com o seu namorado e entao temos de multiplicar por 2 por cada casal.
assim:
5! x 2 x 2 x 2 x 2 x 2 = 5! x 2^5 = 3840
obrigado pela vossa ajuda !
-
Madjer
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Set 10, 2010 09:38
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: formado
Voltar para Tópicos sem Interação (leia as regras)
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema de análise combinatória
por Fernanda Lauton » Seg Mar 29, 2010 17:41
- 5 Respostas
- 5733 Exibições
- Última mensagem por Elcioschin

Sex Abr 09, 2010 11:07
Estatística
-
- Problema de análise combinatória
por RJ1572 » Dom Abr 04, 2010 13:28
- 2 Respostas
- 2899 Exibições
- Última mensagem por RJ1572

Dom Abr 04, 2010 21:27
Estatística
-
- Problema de Análise Combinatória
por roberoliveira » Ter Jun 08, 2010 20:04
- 5 Respostas
- 4376 Exibições
- Última mensagem por angeruzzi

Sex Jun 11, 2010 15:57
Estatística
-
- [analise combinatoria] problema!
por santtus » Qua Fev 20, 2013 02:18
- 1 Respostas
- 2171 Exibições
- Última mensagem por Rafael16

Qua Fev 20, 2013 11:57
Análise Combinatória
-
- Problema de análise combinatória.
por Sobreira » Seg Set 15, 2014 01:03
- 1 Respostas
- 4456 Exibições
- Última mensagem por DanielFerreira

Dom Set 21, 2014 14:12
Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


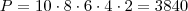



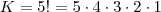 . Porém, cada rapaz pode trocar de lugar com a namorada, ou seja, cada lugar pode trocar 2 vezes:
. Porém, cada rapaz pode trocar de lugar com a namorada, ou seja, cada lugar pode trocar 2 vezes: 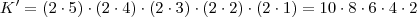 .
.