Como prometi vou postar aqui algumas questões do Vestibular 2008 da UFRGS, terceiro melhor do Brasil, cuja prova de Matemática é considerada a mais Dificel.
Ai vai:
1 - O custo de uma embalagem é diretamente proporcional à superfície do sólido que se deseja embalar. Se o custo para embalar um cubo de 40 cm de aresta é R$10,00, a embalagem de um cubo de 80 cm de aresta custa, em reais,
(A) 15.
(B) 20.
(C) 25.
(D) 40.
(E) 80.
2 - Em março de 2007, o menor preço oferecido por uma companhia telefônica para uma ligação do Brasil para os Estados Unidos era de R$0,95 o minuto. O mesmo serviço pela internet custava R$0,05 o minuto e mais R$0,10 da taxa de conexão da chamada. Em ambas as situações, o preço por segundo correspondia a do preço por minuto.
Nessas condições, para que uma ligação telefônica, do Brasil para os Estados Unidos, tivesse um custo menor via companhia telefônica do que via internet, a duração dessa ligação deveria ser, em número inteiro de segundos, no máximo, de
(A) 6.
(B) 7.
(C) 8.
(D) 9.
(E) 10.
3 - Um hexágono regular tem lado de comprimento 1. A soma dos quadrados de todas as suas diagonais é
(A) 6.
(B) 12.
(C) 18.
(D) 24.
(E) 30.
4 - Numa seqüência de quadrados, o primeiro tem lado igual a 1, e o lado de cada um dos seguintes é igual à diagonal do quadrado anterior.
A soma das áreas dos dez primeiros quadrados dessa seqüência é
(A) 1023.
(B) 1024.
(C) 2047.
(D) 2048.
(E) 4096.
5 - O polinômio p(x)=
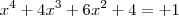 tem
tem(A) apenas duas raízes reais distintas.
(B) apenas duas raízes positivas.
(C) todas as raízes positivas.
(D) quatro raízes iguais.
(E) quatro raízes distintas.
6 - Traçando-se os gráficos das funções definidas por f(x) = 2 sen x e g(x) = 16 -
 e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é(A) 0.
(B) 1.
(C) 2.
(D) 3.
(E) 4.


 Raio = 1
Raio = 1 ![D = \ell\:\sqrt[]{2} D = \ell\:\sqrt[]{2}](/latexrender/pictures/777e9f39975a29b503809d772846b527.png) . Logo você percebe que a área do segundo quadrado é 2, do terceiro é 4, do quarto é 8, ... , caindo numa PG de razão 2. Usando a fórmula da soma de uma PG finita chega-se ao resultado de
. Logo você percebe que a área do segundo quadrado é 2, do terceiro é 4, do quarto é 8, ... , caindo numa PG de razão 2. Usando a fórmula da soma de uma PG finita chega-se ao resultado de 

 então é fácil perceber que:
então é fácil perceber que: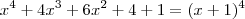
 .
.
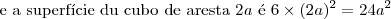


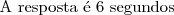






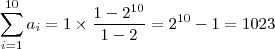

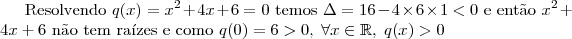


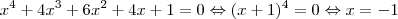
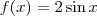 e
e  e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é![\phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0 \phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0](/latexrender/pictures/56cd4f5842222ffa3cf56bea01e2a9e4.png)
![\left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right \left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right](/latexrender/pictures/e541cc339277324141018ac2a21491d7.png)


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.