Texto 1
Nos últimos anos, a Física tem sido uma aliada dos pesquisadores que estudam as obras de arte. Ao examinar pinturas até o detalhe dos átomos com auxílio das técnicas de fluorescência de raios X e de radiografias, ela põe a nu segredos que se escondem debaixo da tinta, caracteriza os pigmentos que compunham a paleta de cada pintor e aponta retoques e desgastes nas telas, orientando futuros trabalhos de restauração.
Para tanto, emprega-se um aparelho que lança um feixe focalizado de raios X num círculo de meio centímetro de diâmetro e produz um processo conhecido como efeito fotoelétrico: enquanto se movimentam para restabelecer o equilíbrio, os elétrons também emitem raios X – os chamados raios X característicos, que o equipamento detecta e reproduz na tela do computador na forma de curvas de emissão de energias. A energia emitida é característica para cada elemento químico e, de posse dessa informação, pode-se inferir o pigmento usado naquele ponto do quadro.
Figura: equipamento portátil esquadrinha o quadro Moisés e Jocabed, de Pedro Américo.
Fonte: Revista Pesquisa Fapesp. ed 199, Set. 2012
Dados: Energia do fóton:
, 
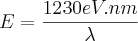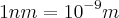, Carga elementar = 
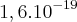C, Constante de Planck h =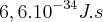 
1. Com base no texto 1, afirma-se que:
a) ao atingir os cristais de metal da tela, os fótons de raios X produzem o efeito fotoelétrico, efeito esse que é explicado pelo comportamento ondulatório da luz.
b) a frequência dos raios X que incidem na obra de arte apresenta valor menor que a frequência das microondas empregadas nos radares de trânsito.
c) quando um fóton de raios X de comprimento de onda igual a 1 nm atinge um cristal de cobalto, cuja função trabalho é 5 eV, a energia cinética máxima dos elétrons emitidos é aproximadamente igual a
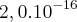J.d) a energia cinética dos fotoelétrons depende da frequência e da intensidade da radiação incidente nos cristais da obra de arte.
e) quando os raios X incidentes atingem um cristal de chumbo, cuja função trabalho é
J, a frequência de corte para o efeito fotoelétrico é igual a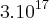 
Hz.Tentativa de Resolução;
Caso comentem principalmente a alternativa "e)", fico grato. Sobre as outras, consigo discernir bem se estão certas ou erradas. A letra "c)" é a correta em síntese.
Gabarito Preliminar: C
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.