Fala campeão, vamos "detonar" esse problema também ? Para fechar a noite bem....
Vamos definir as variáveis (engraçado, acho que já disse isso antes...), o número de crianças será x e o número total de bombons será y, definido isso, vamos ao problema....
"...Distribuindo-se certa quantidade de bombons para um grupo de crianças,recebendo cada uma 5 bombons(sic)...", campeão, se cada criança recebe 5 bombons, o número de bombons total será o produto do número de bombons de cada criança pelo número de cada criança, veja:
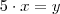
"...Entretanto,se resolvessemos da 7 bombons para cada criança,ficariam 4 crianças com um bombom cada(sic)...", aqui temos a seguinte situação, daremos 7 bombons para cada criança sendo que 4 delas ficarão com 1 bombom cada, logo o número de crianças que receberá 7 bombons será o número total de crianças menos o número de crianças que ficarão com 1 bombom cada

, então para termos o total de bombons temos que somar o número de bombons das 4 crianças, logo:
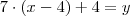
Lembre-se,

é o número de crianças que irá receber os 7 bombons, isto é, o total de crianças, x, menos as 4 que receberão 1 bombom cada. Mas

só me diz quantos bombons teremos quando dermos os 7 bombons para as crianças, para termos o total de bombons da caixa temos que somar os 4 bombons das crianças que só receberão 1 bombom cada, isto é, 4 crianças, então a equação fica daquele jeito.
Agora vamos igualar as equações:
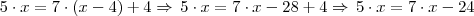
Arrumando a casa passando letras para um lado e números para o outro, teremos:

Logo o número de crianças é 12, então o número de bombons será

Espero ter ajudado..
Abs,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...




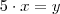
 , então para termos o total de bombons temos que somar o número de bombons das 4 crianças, logo:
, então para termos o total de bombons temos que somar o número de bombons das 4 crianças, logo: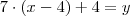
 é o número de crianças que irá receber os 7 bombons, isto é, o total de crianças, x, menos as 4 que receberão 1 bombom cada. Mas
é o número de crianças que irá receber os 7 bombons, isto é, o total de crianças, x, menos as 4 que receberão 1 bombom cada. Mas  só me diz quantos bombons teremos quando dermos os 7 bombons para as crianças, para termos o total de bombons da caixa temos que somar os 4 bombons das crianças que só receberão 1 bombom cada, isto é, 4 crianças, então a equação fica daquele jeito.
só me diz quantos bombons teremos quando dermos os 7 bombons para as crianças, para termos o total de bombons da caixa temos que somar os 4 bombons das crianças que só receberão 1 bombom cada, isto é, 4 crianças, então a equação fica daquele jeito.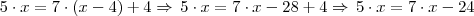




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
