Boa noite, Raphael.
É claro que com a resposta fica mais fácil de chegar a esta conclusão, mas eu pensaria assim:
Achar o numero de dois algarismo__
A__ __
B__
no qual 5 vezes os algarismo das dezenas,menos duas vezes o algarismo das unidades e igual a 7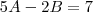
Perceba que o
A obrigatoriamente é ímpar, já que
2B é par; e para uma subtração dar ímpar um deles tem que ser ímpar.
Fazendo

, temos que para satisfazer o enunciado,

, pois
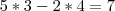
Mas,
invertendo-se a ordem dos algarismo, NÃO obtem-se o numero que excede ao primeiro de 36:Pois pelos número que pegamos

(e não 36 como queremos).
Fazendo o mesmo procedimento, agora para

, temos que para satisfazer o enunciado,

, pois
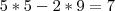
E,
invertendo-se a ordem dos algarismo, obtem-se o numero que excede ao primeiro de 36:ois pelos número que pegamos

(como queremos).

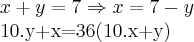


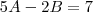
 , temos que para satisfazer o enunciado,
, temos que para satisfazer o enunciado,  , pois
, pois 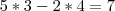
 (e não 36 como queremos).
(e não 36 como queremos). , temos que para satisfazer o enunciado,
, temos que para satisfazer o enunciado,  , pois
, pois 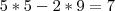
 (como queremos).
(como queremos).


 .
.



